Deep-learning inversion: a next generation seismic velocity-model building method

• arxiv链接：arxiv.org/abs/1902.06267

• 传统方法通过层析成像或者FWI直接获取地址速度，但是这种方法太耗时且资源消耗大，并且依赖人工交互来控制质量。这篇论文提出了一种基于监督学习深度全卷积神经网络，直接从地震图中构建速度模型（Velocity-Model Building）。该方法与传统方法的最大区别便是其基于大数据训练而不是先验知识假设。

速度模型构建（VMB）

• 在整个地震勘探过程中（地震数据采集、处理、解释）中都需要用到速度模型，良好的速度模型是构建reverse-time migration（逆时偏移）和地震成像技术的前提。

层析成像

• 这里简单了解了一下层析成像。

  地震层析成像就是通过对观测到的地震波各种震相进行分析，反推处地下介质的速度结构以及其他物理参数。

  在具体分析中又分为正演和反演两种技术，正演是已知地震源、地球模型和地震波传播理论，来模型地震波在地球中的传播过程，一般用于验证地震模型的准确性和理解地震波的传播特性。

  反演则是利用实际观测地震数据，根据地震波的传播时间、振幅、频率等反推地球内部不同位置的密度、速度、衰减等，揭示地球内部构造和性质。

全波形反演（FWI）

• 全波形反演便是其中的一种反演技术。具体的做法便是正演得到一个速度模型，再将这个模型和实际观测模型对比计算差异，通过反演算法更新速度模型，也就是一个迭代的过程。

  非常类似机器学习的训练过程。

FCN-BASED INVERSION METHOD

基本反演问题

• 恒定密度二维声波方程为

  $$\frac{1}{v^2(x, z)} \frac{\partial^2 u(x, z, t)}{\partial t^2} = \nabla^2 u(x,z,t) + s(x,z,t)\tag{1}$$

  这里用$(x,z)$表示空间位置，$t$代表时间，其中$v$表示纵波速度，$u$代表波振幅，$\nabla^2(\cdot)$为拉普拉斯算子，有

  $$\nabla^2(\cdot) = \frac{\partial^2(\cdot)}{\partial x^2} + \frac{\partial^2(\cdot)}{\partial z^2}$$

  $s$代表信号源。

• 方程1中通常有$u=H(v)$，其中$H(\cdot)$死一个非线性映射。传统反演方法的目的是最小化如下目标函数值

  $$\bar{v} = \arg \min\limits_v f(v) = \arg\min\limits_v \frac{1}{2}\lVert H(v) - d\rVert_2^2 \tag{2}$$

  其中$d$是实际测量的地震数据，$\lVert\cdot\rVert_2$代表L2范数（欧式长度），$f(\cdot)$代表数据保真度残差（data-fidelity residuals）。

• 在大部分应用中使用一个快速且精确的逆算子$\nabla^{-1}$来解决上述式2。在地震速度模型问题中，如果$d$包含全波形信息，则上述方程就是FWI。

回顾FCN

• FCN方法可以表示为

  $$y = Net(x;\Theta) = S(K_2*(M(R(K_1*x + b_1))) + b_2)\tag{3}$$

  其中$Net(\cdot)$表示FCN网络，$(x,y)$代表输入输出，$\Theta = \{K_1, K_2, b_1, b_2\}$代表学习的参数集（卷积权重和偏置）。$R$是非线性激活函数，$M$代表下采样函数，$S$代表Softmax函数（归一化）。

数学框架

• 为了将地震数据作为输入来估计速度模型，需要将地震数据从数据域$(x,t)$投影到$(x,z)$。

  

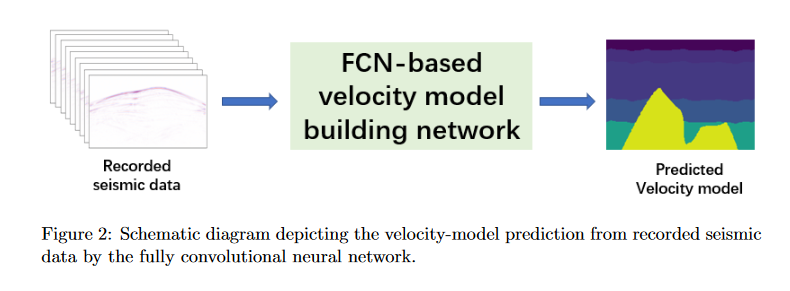
  如上图所见，需要建立一个输入和输出之间的映射，可以表示为

  $$\widetilde{v} = Net(d;\Theta)\tag{4}$$

  其中$d$代表原始地震数据，$\widetilde{v}$表示网络预测的P波速度模型。具体方法分为两步：训练和预测。具体如下图所示：

  

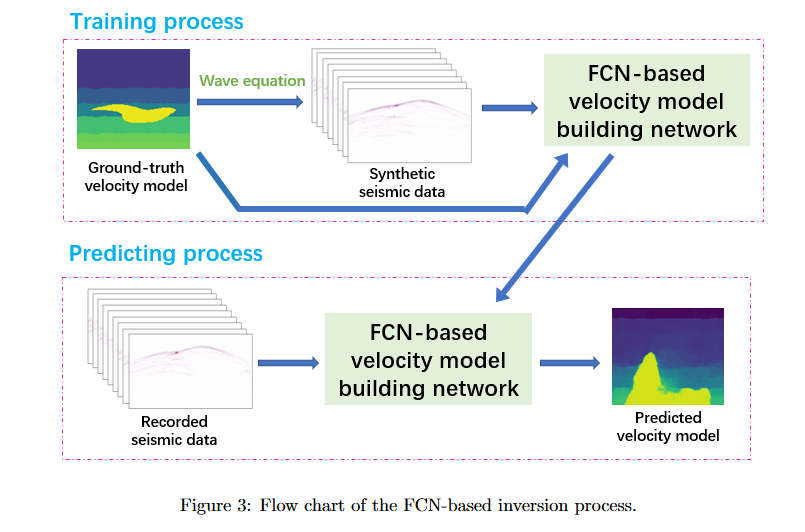
  在训练之前需要生成多个速度模型作为输出$v_n$，然后应用声波方程作为前向模型生成合成地震数据作为输入$d_n$。训练时用$\{d_n,v_n\}_{n=1}^N$作为一组映射输入给网络学习。

• 训练的目标是拟合一个从地震数据输入到真实速度模型的非线性函数。也就是不断的优化目标函数值

  $$\widehat{\Theta} = \arg \min\limits_{\Theta}\frac{1}{mN}\sum_{n=1}^NL(v_n,Net(d_n;\Theta))\tag{5}$$

  其中$m$表示速度模型的总像素量，$L(\cdot)$代表真实值$v_n$和预测值$\widetilde{v}_n$之间的误差，在实验中误差用L2范数计算。

• 为了更新学习参数$\Theta$，可以使用BP和SGD进行优化。实际训练时因为训练集很大，直接计算$\nabla_\Theta L(d;\Theta)$不太可行，所以使用小批次尺寸的$h$计算$L_h$近似梯度（每次迭代选取一部分计算误差）。所以此时目标函数变成

  $$\widehat{\Theta} = \arg\min\limits_{\Theta}\frac{1}{mh}L_h = \arg\min\limits_{\Theta}\frac{1}{mh}\sum_{n=1}^h\lVert v_n - Net(d_n;\Theta)\rVert_2^2\tag{6}$$

  其中真实速度模型$v_n$在训练时是已知的，测试时是未知的。在实际训练时损失函数与FWI方法即式2不同，因为FWI中损失计算的是地震图和模拟地震图之间的平方差，而这里使用Adam算法（SGD的变形），参数更新方程如下：

  $$\Theta_{t+1} = \Theta_t - \delta g(\frac{1}{mh}\nabla_\Theta L_h(d_n;\Theta;v_n))\tag{7}$$

  其中$\delta$代表正向步长。该算法非常适合处理大数据/参数问题。

网络架构

• 为了实现从原始地震数据自动进行地震VMB，这里使用并修改了UNet（基于FCN的变形）。详细结构如图

  

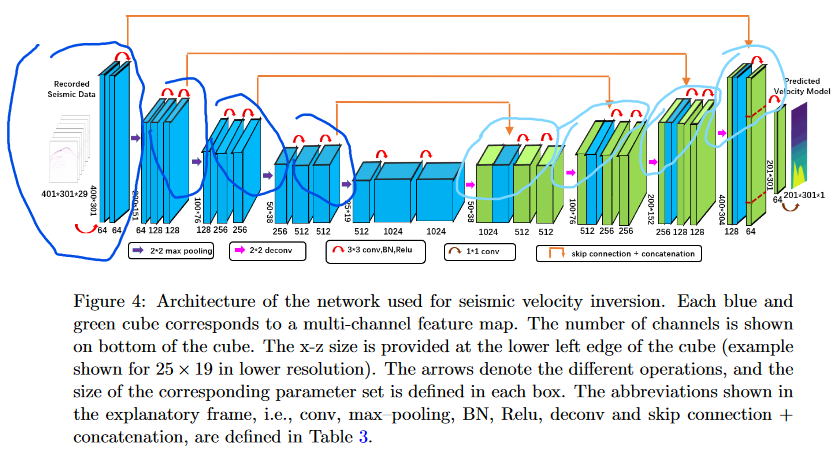
• 算法1：基于FCN的反演

  输入：$\{d_n\}_{n=1}^N$：地震数据，$\{v_n\}_{n=1}^N$：速度模型，T：轮次，$lr$：网络学习率，$h$：批次大小，$num$：训练集数目。

  符号说明：$*$：二维卷积（填充0），$*_\uparrow$：二维反卷积，$R(\cdot)$：ReLU，$B(\cdot)$：归一化操作，$M(\cdot)$：最大值池化操作，$C(\cdot)$：复制并连接，$\Theta = \{K,b\}$：学习参数，$L$：损失函数，$Adam$：SDG算法。 初始化：$t=1,loss=.0,y_0 = d$

  训练过程：

  1. 生成相似地质结构的不同速度模型；
  2. 使用有限差分法合成地震数据；
  3. 将数据输入至网络，并使用Adam算法更新参数。

  

  训练算法伪代码

  预测过程：

  1. 与训练过程相同，合成不同速度模型的地震数据；
  2. 将地震数据输入到网络中进行预测。

  输出：预测速度模型$v^{*}$

NUMERICAL EXPERIMENTS AND RESULTS

数据集

• 这里使用了2维模拟速度模型核三维SEG盐体模型中提取的2维模型（https://s3.amazonaws.com/open.source.geoscience/open_data/seg_eage_models_cd/salt_and_overthrust_models.tar.gz）

• 为了证明深度学习在地震波形反演中的可用性，先生成了具有光滑界面曲率的随机速度模型，随着深度增加而增加速度。这里每个模型有5到12层，每层的波速范围为2km/s到4km/s。然后将一个随机形状的盐体（无机矿物）插入到模型的随机位置，每个盐体波速为4500m/s的恒定值。

  每个速度模型大小为$x\times z=201\times 301$，空间间隔为$\Delta x = \Delta z = 10m$（也就是每个像素代表10m）

  

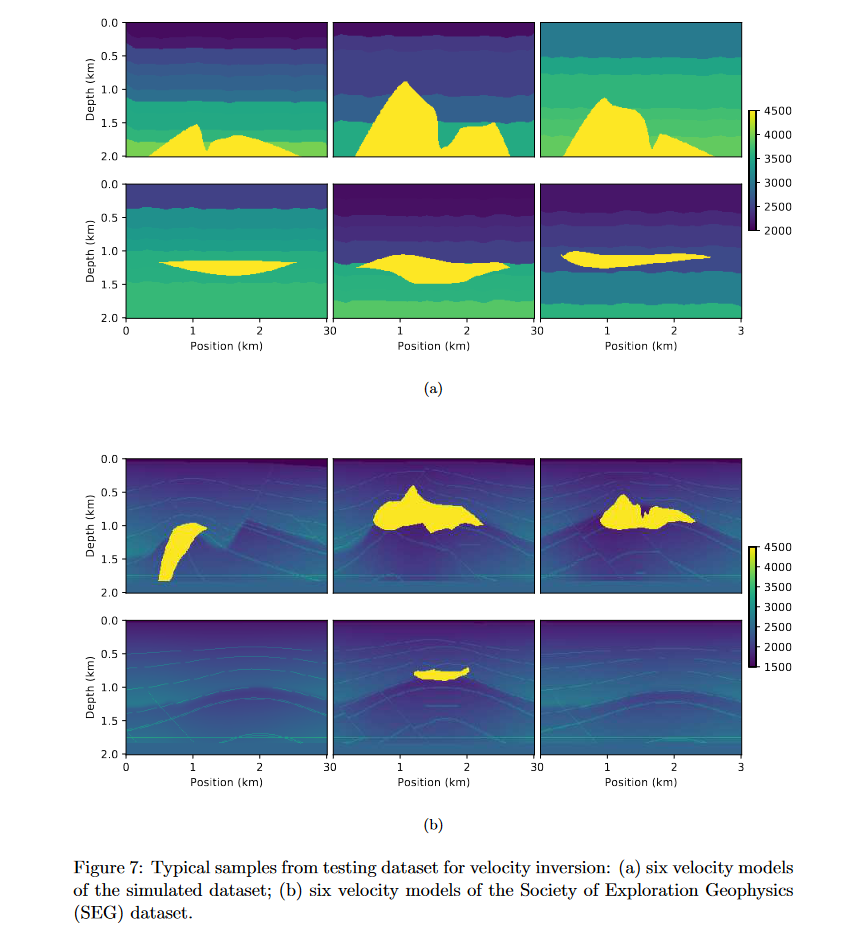
  这是模拟的速度模型和SEG中的速度模型对比。

• 最后一共制作了1600个模拟速度模型，再从SEG的三维盐体模型中提取了130个速度模型。

• 为了求解声波方程，论文采用时域交错网格有限差分方法（time-domain stagger-grid finite-difference scheme），该方法使用二阶时间近似和八阶空间近似（这里的阶代表精度，例如用二阶泰勒展开去近似时间导数）。对于每个速度模型均匀地放置了29个震源，依次模拟炮击再由301个接收器记录地质数据。具体参数为：

  

  最后使用完美匹配层（perfectly matched layer，PML）方法吸收边界条件，减少左、右和底部边缘的非物理反射。为了验证网络稳定性，对每个测试地震数据添加均值为0，标准偏差为5%的高斯噪声（$\mu = 0, \sigma=0.05$），并使地震数据振幅提高两倍。

• 测试数据集：用同样方法得到100个模拟地震数据和10个SEG盐体模型。

模拟集上的反演

• 每个批次随机选择10个$201\times 301$速度模型样本，每对数据（地震数据，速度模型）中单次地震数据维度下采样至$400\times 301$，然后开始训练，具体参数如下：

  

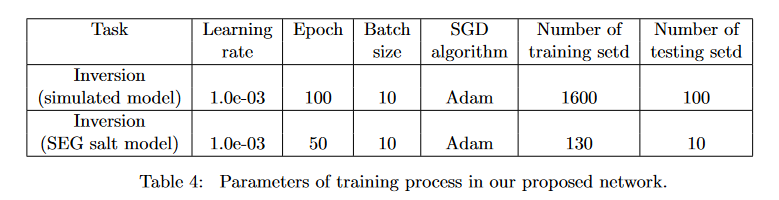
  同时这里将高斯平滑函数平滑的真实速度模型作为初始速度模型进行训练。得到的结果为：

  

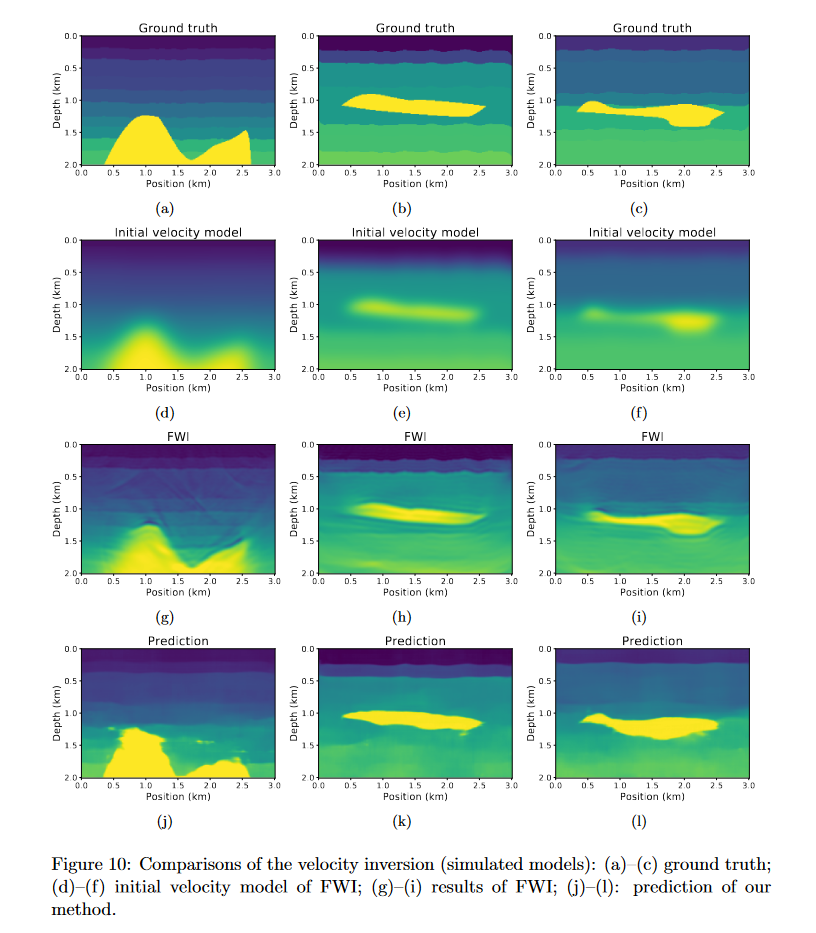
  （这里文中提到对一个模型FWI反演需要37分钟GPU时间，而花了1078分钟训练出来FCN反演网络后每次预测只需要2秒。）

• 后续还测试了对添加噪声/振幅加倍的数据进行预测，得到的结果为

  

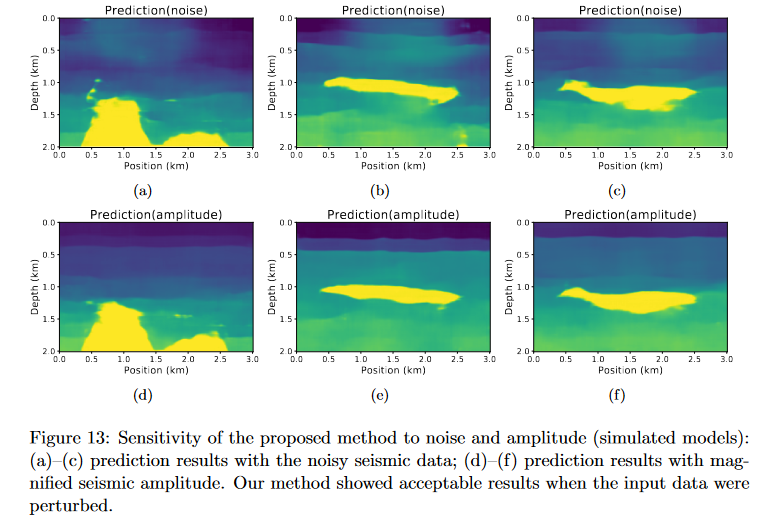
  这里发现噪音对网络的预测影响很大（图中明显看出分层受到影响），而振幅加倍的影响几乎没有，然后文中在这里描绘了下未来可以试试对其他类型噪声的测试。

SEG数据集上的反演

• 这里将模拟数据集训练的网络作为初始化网络，来训练SEG盐体数据集，在50个周期内将损失收敛到0。注意这里的FWI反演对比依然使用高斯平滑函数作为初始速度模型。

  得到的结果如下：

  

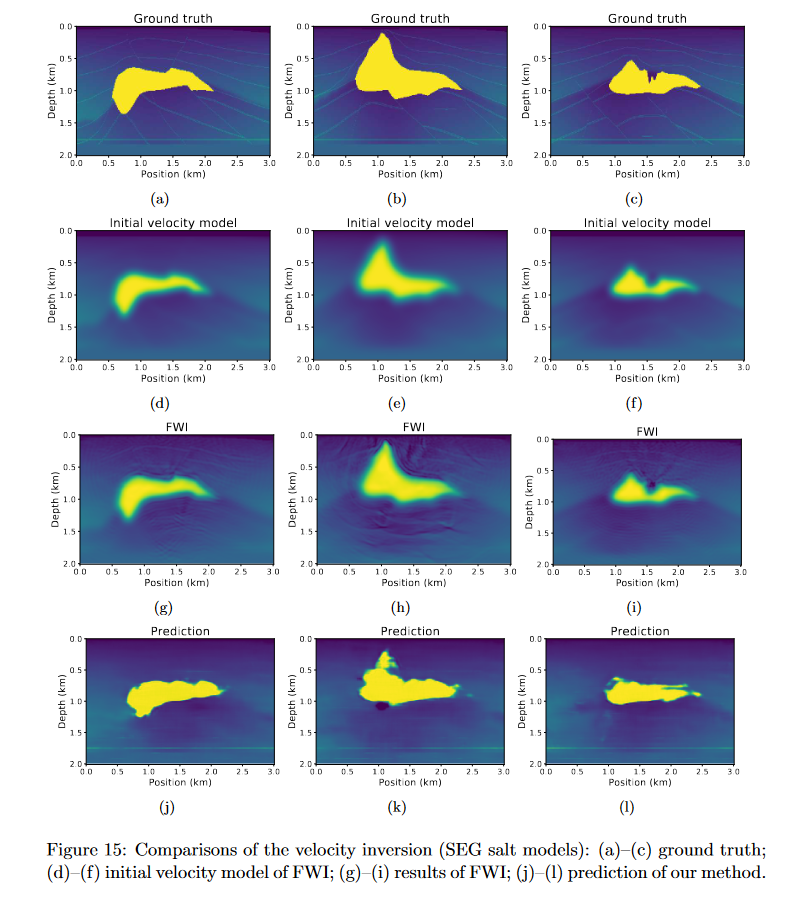
  这里可以看到预测的效果还没有FWI好，文中猜测是由于数据集太少导致。

• 同样对SEG数据也进行了噪声/振幅加倍测试

  

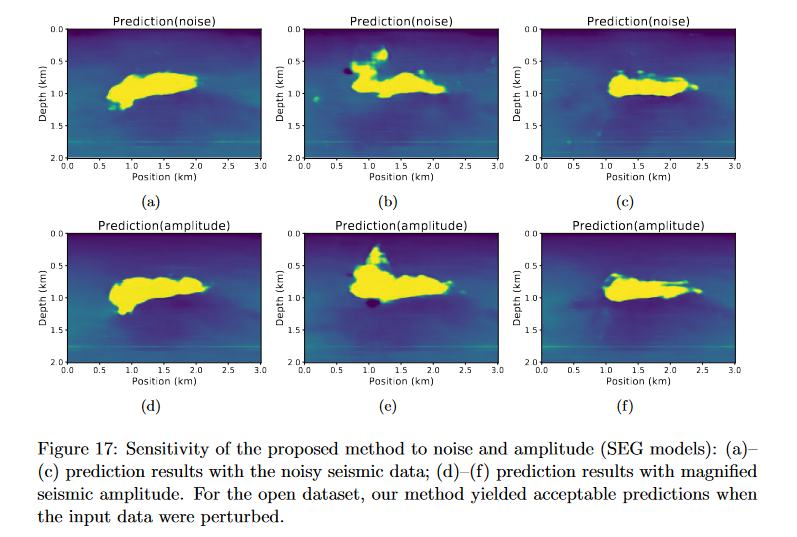
  结果和模拟集上噪音/振幅的影响类似，噪音影响比较大，振幅影响还好。

• 两种训练集训练时误差（这里用的MSE）变化如下：

  

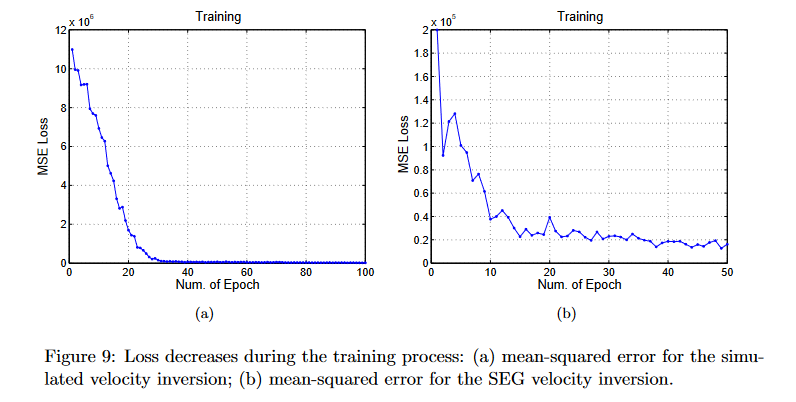
• 虽然最终结果不比FWI好很多，但是至少说明这种方法是可行的，可以直接从原始地震数据中反演而无需初始速度模型。同时即使存在扰动（噪声之类的）也可以有效得到一个近似非线性映射关系，同时比传统的FWI方法快多了，因为不需要搜索迭代最优解。主要的计算成本在训练阶段，预测成本忽略不计。

讨论

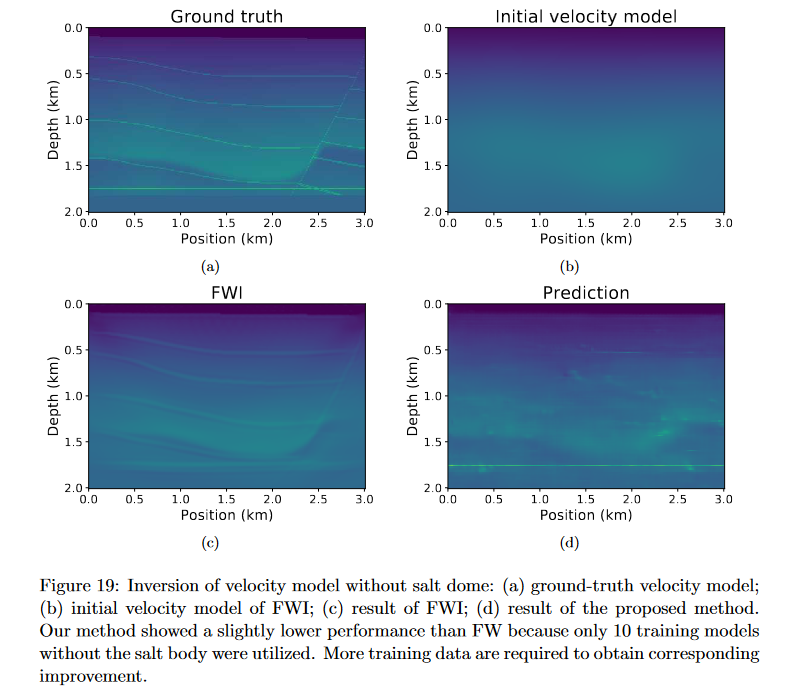
1. 训练数据集对网络质量的影响？

   当训练模型和预测模型包含相似结构或特征时网络效果才会更好，所以需要更大的训练样本，并且发现本文的网络更适合提取盐体特征，文中使用了不含盐体的数据进行预测，结果比FWI性能要低，如图：

   

2. 当测试数据中确实低频时如何应用网络？

   缺少低频的实际数据是FWI实际应用的一个主要问题，在机器学习中可以先从模拟数据或先验信息数据中学习“低频”。

   这里文中给出了当低频（0到1/10的归一化傅里叶频谱）通过傅里叶变换和高通滤波器移除后的预测效果

   

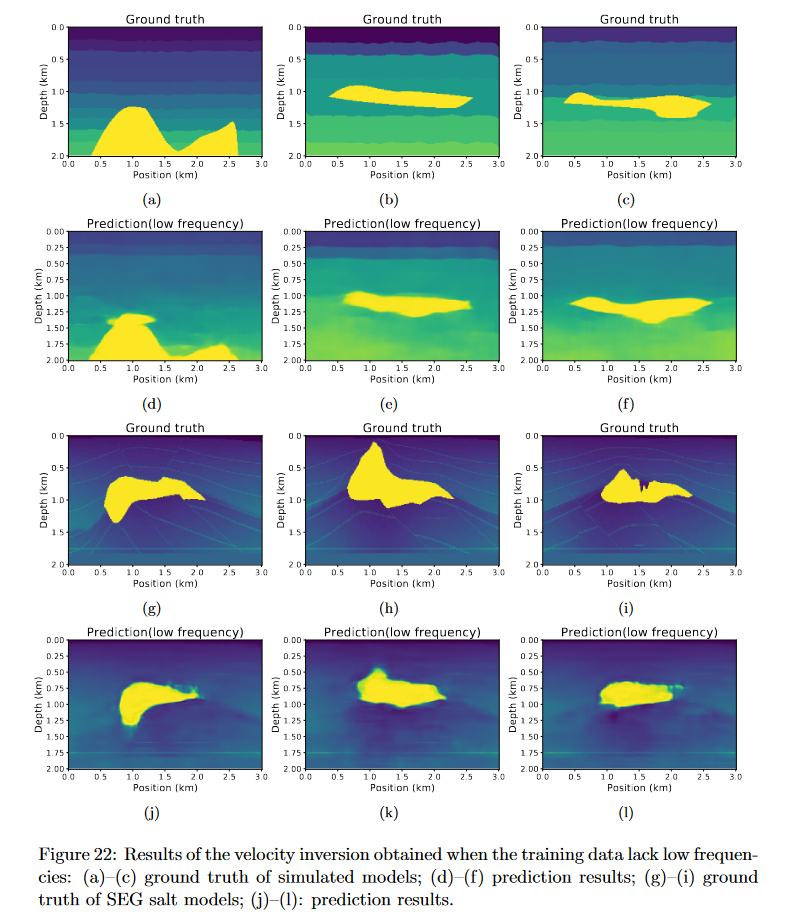
   可以发现边界不清晰，背景也比较模糊。同时这里使用缺少低频的训练集重新训练网络后得到效果稍好。也说明了训练集对网络的重要性。

个人总结

• 该文使用UNet实现直接对原始地震数据进行反演得到精确的速度模型。

  然后使用模拟数据和SEG数据训练模型和FWI方法做了对比。