InversionNet: An Efficient and Accurate Data-Driven Full Waveform Inversion

• DOI: 10.1109/TCI.2019.2956866

• 传统的FWI很贵且效率不高，本文提出了一种深度学习反演方法，利用神经网络（CNN）学习和预测地震速度和地下结构的关系构建地震速度模型。

背景

物理驱动技术

• 时域中的声波方程为

  $$\left[\frac{1}{K(\boldsymbol{r})}\frac{\partial^2}{\partial t^2} - \nabla\cdot\left(\frac{1}{\rho(\boldsymbol{r})}\nabla\right)\right]p(\boldsymbol{r},t) = s(\boldsymbol{r},t)\tag{1}$$

  其中$\boldsymbol{r}$是位置向量，$\rho$代表密度，$K$是体积模量，$s$代表震源，$p$为压力波场，$t$为时间。正演表示为

  $$P = f(\boldsymbol{y})\tag{2}$$

  其中$P$代表波场位移，$f$代表正演操作，$\boldsymbol{y}$代表速度模型向量（密度和波速）。使用时域交错网格有限差分来求解。同时本文只关注恒定密度+弹性介质的情况。

• 对于反演，便可以看成一个优化问题，最小化目标函数

  $$E(\boldsymbol{y}) = \min\limits_{\boldsymbol{y}}\left\{\lVert\boldsymbol{x} - f(\boldsymbol{y})\rVert_2^2 + \lambda R(\boldsymbol{y})\right\}\tag{3}$$

  其中$x$代表真实记录的数据，$f(\boldsymbol{y})$代表正演结果，$\lVert\cdot\rVert_2$代表L2范式，$\lambda$是正则化惩罚参数，$R(y)$为正则项，常用Tikhonov正则项（总方差正则化、岭回归、TV）

  $$E(\boldsymbol{y}) = \min\limits_{\boldsymbol{y}}\left\{\lVert\boldsymbol{x} - f(\boldsymbol{y})\rVert_2^2 + \lambda \lVert H\boldsymbol{y}\rVert_2^2\right\}\tag{4}$$

  其中$H$为高通滤波矩阵或单位矩阵。TV正则项为L2正则项，非常适合平滑模型。

• 最终添加TV正则项的目标函数为

  $$E(\boldsymbol{y}) = \min\limits_{\boldsymbol{y}}\left\{\lVert\boldsymbol{x} - f(\boldsymbol{y})\rVert_2^2 + \lambda \lVert\boldsymbol{y}\rVert_{\mathrm{TV}}\right\}\tag{5}$$

  其中在2维模型中正则项为

  $$\lVert\boldsymbol{y}\rVert_{\mathrm{TV}} = \sum_{1\le i,j\le n}{\sqrt{\lvert (\nabla_x \boldsymbol{y})_{i,j}\rvert^2 + \lvert(\nabla_z \boldsymbol{y})_{i,j}\rvert^2}}\tag{6}$$

  其中$\lvert (\nabla_x \boldsymbol{y})_{i,j}\rvert = m_{i+1,j} - m_{i,j},\ \lvert (\nabla_z \boldsymbol{y})_{i,j}\rvert = m_{i,j+1} - m_{i,j}$代表网格点$(i,j)$处的方向导数。

• 后面还介绍了对于正则化参数$\lambda$的大小分析，以及MTV正则化技术，并且指出FWI基于梯度优化方案，成本高且对于小型结构的分辨率不够好。

数据驱动技术

• 这便是本文的重点，直接从数据中得到速度模型而不是基于物理方法。和传统FWI的不同就是这种方法需要大量的数据训练模型来保证预测的准确性。

方法

• FWI中的正演模型可以简单表示为

  $$f(\boldsymbol{y}) = \boldsymbol{x}\tag{7}$$

  其中$f$是传播算子，$\boldsymbol{y}$是地质模型，$\boldsymbol{x}$是地震数据。本文的数据驱动方法便是通过CNN近似拟合了$f^{-1}$，再通过局部链接CRF进一步细化输出。

• 因为目标是将数据从一个域转移到另一个域，本文将CNN设计成编码-解码架构。编码器用于提取数据中的高级特征并降低数据维度。解码器用于将这些特征转换到其他域上，具体架构如图1所示。

  

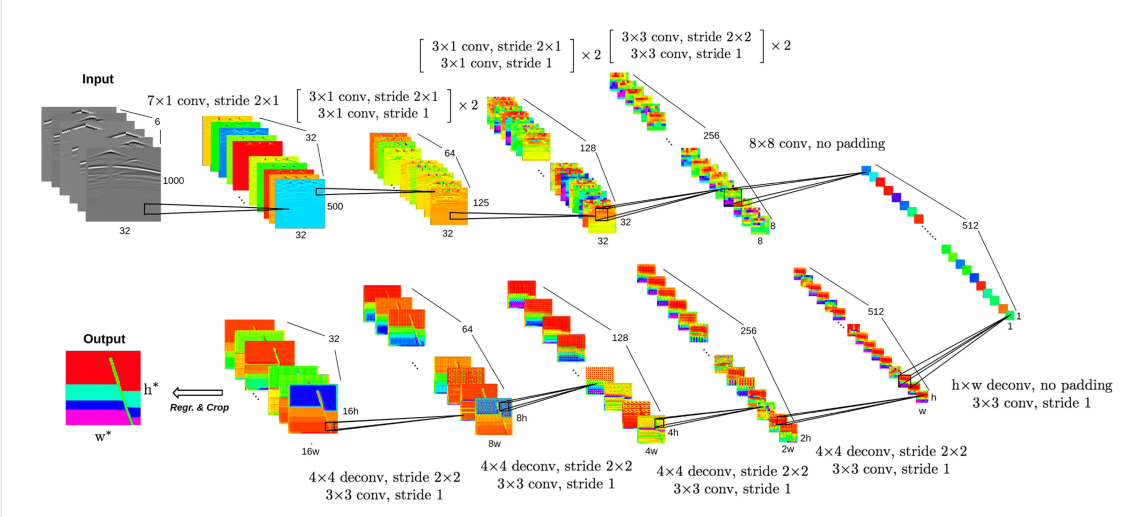
  图1. CNN网络架构

  可以看到这里的编码器用了四层卷积把$1000\times 32 \times 6$变成$8\times 8 \times 256$在变为一维张量。解码器再进行上采样变回指定尺寸。

编码器

• 编码器中包括一组卷积块，每块可以表示为

  $$\boldsymbol{x} = \mathrm{ReLU}(\mathrm{BN}(\mathrm{Conv}(\boldsymbol{x}^{(l)})))\tag{8}$$

  $$\mathrm{Conv}(\boldsymbol{x})_{i,j} = \sum_m\sum_n\sum_c{K_{m,n,c}\cdot \boldsymbol{x}_{(s-1)\times i + m, (s-1)\times j+n, c}}\tag{10}$$

  其中$K\in R^{m\times n\times c}$为卷积核，$s$代表步长。$\mathrm{BN}$为归一化操作

  $$\mathrm{BN}_{\gamma,\beta}(\boldsymbol{x}_{i,j,c}) = \gamma\left(\frac{\boldsymbol{x}_{i,j,c} - \mu_{\mathcal{B}}}{\sqrt{\sigma^2_{\mathcal{B}} + \epsilon}}\right) + \beta\tag{11}$$

  其中$\mu_{\mathcal{B}},\sigma_{\mathcal{B}}$为特征图的平均值和方差（用一个小批次计算），$\epsilon$是一个小常数。

解码器

• 解码器包含多种卷积和反卷积操作进行上采样，这里使用$4\times 4$的卷积核进行反卷积将分辨率提高一倍，再使用$3\times 3$的卷积核进行卷积细化上采样的特征图。最终使用L1损失函数计算误差

  $$\mathrm{L1}(\boldsymbol{y}, \boldsymbol{z}) = \frac{1}{n}\sum_{i=1}^n{\lvert y_i - z_i\rvert}\tag{12}$$

  其中$\boldsymbol{y} = \{y_1,\dots,y_n\}$为真实数据，$\boldsymbol{z} = \{z_1,\dots,z_n\}$为模型预测数据。

条件随机场

• 条件随机场（Conditional Random Fields，CRF）是用来细化模型精度的技术。L1损失训练的CNN不能对每个位置之间的相互关联进行建模，所以不能完全捕捉速度模型的结构特征，为了更好的反映地质结构，本文构建了一个局部链接的CRF用于进一步精细化。

  CRF由Gibbs分布定义为

  $$P(\boldsymbol{y}|\boldsymbol{m}) = \frac{1}{Z(\boldsymbol{m})}\mathrm{exp}(-E(\boldsymbol{y}|\boldsymbol{m}))\tag{13}$$

  $$E(\boldsymbol{y}|\boldsymbol{m}) = \sum_{c\in C(\mathcal{G})}{\phi_c(\boldsymbol{y}_c|\boldsymbol{m})}\tag{14}$$

  $$Z(\boldsymbol{m}) = \int_y{\mathrm{exp}(-E(\boldsymbol{y}|\boldsymbol{m}))\mathrm{d}\boldsymbol{y}}\tag{15}$$

  其中$\boldsymbol{m} = \{\boldsymbol{m}_1,\dots,\boldsymbol{m}_n\}$为变量，$\mathcal{G} = (\mathcal{V}, \mathcal{E})$为定义在$\boldsymbol{m}$上的一组团（clique）为$C(\mathcal{G})$的图，每个团$c$的势（pontential）为$\phi_c$。$E(\boldsymbol{y}|\boldsymbol{m})$代表对所有势求和的能量函数，$Z(\boldsymbol{m})$为归一化常数。

• CRF的参数将使用最大化后验（MAP）$\log{P(\boldsymbol{y}|\boldsymbol{m})}$进行优化

  $\boldsymbol{m}$将遍历尺寸为$n$的所有速度模型，$\boldsymbol{y}$遍历所有可能速度值。速度值以隐式条件地包含于每个速度模型中。CRF的能量函数由一个一元势函数$\phi_u$和一个成对势函数$\phi_p$组成：

  $$E(\boldsymbol{y}|\boldsymbol{m}) = \sum_{i\in \mathcal{V}}{\phi_u(y_i|\boldsymbol{m})} + \sum_{i\in \mathcal{V}}\sum_{j\in \mathcal{N}_i}{\phi_p(y_i,y_i|\boldsymbol{m})}\tag{16}$$

  其中$\mathcal{N}_i$为与$y_i$相连的节点集合。一元势函数对输入和每个独立输出$y_i$建立映射关系。成对势函数对输出$y_i$与$y_j$两两建立联系。定义如下

  $$\phi_u(y_i|\boldsymbol{m}) = (y_i - z_i)^2\tag{17}$$

  $$\phi_p(y_i,y_j|\boldsymbol{m}) = \omega \cdot K_{ij}(y_i - y_j)^2\tag{18}$$

  其中$z_i,\dots,z_n$为CNN输出的速度预测值，$\omega$为学习权重，$K_{ij}$为相似矩阵，有

  $$K_{ij} = \exp(-\lambda_1\lVert \mathbf{I}_i - \mathbf{I}_j\rVert^2 - \lambda_2\lVert \mathbf{p}_i - \mathbf{p}_j\rVert^2)\tag{19}$$

  其中$\mathbf{I}$为解码器生成的最终特征图的特征向量，$\mathbf{p}$为位置向量，$\lambda_1,\lambda_2$为超参数（hypeparameters，指人工调节的参数）。简单的说便是两个不同的节点如果特征、位置近似的话$K_{ij}$就越大，从而势函数值越大。

• CRF中$E$与$P$负相关，即$E$越小越好，预测的位置越准确一元势越小，且两个相似节点的预测也相近的话则成对势也越小，则$E$越小。而如果相邻节点预测值不同则惩罚将变大即$E$变大。

近似推导

• 具体计算的时候不会直接式13、式16求解，因为涉及求大矩阵的逆，复杂度为$O(n^3)$。所以一般使用均值场理论（MFT）来计算分布$Q$，$Q$满足$Q(\boldsymbol{y}|\boldsymbol{m}) = \prod_i Q_i(y_i|\boldsymbol{m})$，且$P$和$Q$之间KL散度最小。此时有

  $$\log Q_i(y_i|\boldsymbol{m}) = \mathbb{E}_{j\in\mathcal{N}_i}[\log P(\boldsymbol{y}|\boldsymbol{m})] + \mathrm{const}\tag{20}$$

  其中$\mathbb{E}_{j\in\mathcal{N}_i}$为分布$Q_j$在$j\in\mathcal{N}_i$下$\log P$的期望。

• 联立式13、式16、式17、式18和式20有

  $$\begin{aligned} \log Q_i(y_i|\boldsymbol{m}) &= (y_i - z_i)^2 + \omega \sum_{j\in \mathcal{N}_i}{K_{ij}(y_i - y_j)^2}\\ &=\left(1+\omega\sum_{j\in\mathcal{N}_i}{K_{ij}}\right)y_i^2 - 2\left(z_i+\omega\sum_{j\in\mathcal{N}_i}{K_{ij}\mathbb{E}[y_j]}\right)y_i + \mathrm{const} \end{aligned}\tag{21}$$

  由于$Q_i$是关于$y_j$的二次函数，所以它可以被高斯分布表示

  $$\mu_i = \frac{z_i + \omega\sum_{j\in \mathcal{N}_i{K_{ij}\mu_j}}}{1 + \omega\sum_{j \in\mathcal{N}_i{K_{ij}}}}\tag{22}$$

  $$\sigma_i^2 = \frac{1}{2(1+\omega\sum_{j\in\mathcal{N}_i}{K_{ij}})}\tag{23}$$

  由于$K_{ij}>0$，所以这里令$\omega>0$使得$Q_i$为有效分布。最后使用式22、式23迭代计算$Q_1, \dots, Q_n$直到满足收敛准则为止，其中使用单次预测值$z$作为$\mu$的初始值。

• 最后对每个因子分布$Q_i$执行MAP得到$y_i$，有

  $$\begin{aligned} y_i &= \argmax\limits_{y_i}{Q_i(y_i|\boldsymbol{m})}\\ &= \mu_i \end{aligned}\tag{24}$$

训练

• 这里的目标是找到参数$\omega$使得最大化$\log{P(\boldsymbol{y}|\boldsymbol{m})}$，通过上述的近似推导得到损失函数为

  $$\mathcal{L}(Q;\omega) = \sum_{i\in \mathcal{V}}{\log Q_i(y_i|\mathbf{m})}\tag{25}$$

  通过投影梯度上升法得到$\omega$的递推公式为

  $$\omega^{(k+1)} = \max\left(0, \omega^{(k)}+\alpha \frac{\partial \mathcal{L}(Q;\omega^{(k)})}{\partial \omega^{(k)}}\right)\tag{26}$$

  其中$\alpha$为学习率，$\omega^{(0)}$为0。

总结

1. 一种端到端的编码器-解码器架构。
2. 输入的地震数据高宽比过大，优先压缩高度，不过这导致丢失时空相关性。
3. 引入CRF理论优化网络，使用MFT进行实际计算。