Deep Learning for Low-Frequency Extrapolation of Multicomponent Data in Elastic FWI

• DOI: 10.1109/TGRS.2021.3135790

• FWI的成功强依赖于一个准确的初始模型，在弹性体制下尤为重要——由于S-波波长较短，弹性FWI中的周期跳跃现象比声波FWI更严重。本文中，作者通过提出合成多分量弹性低频地震记录，并将这些“人工” 低频数据作为弹性FWI的频率扫描种子，进一步扩展了外推弹性FWI的工作。作者的方案包含深度学习——可以在两个训练数据集上训练同一个卷积神经网络（CNN），一个是粒子速度的垂直分量，另一个是水平分量，或将两个分量放在一起训练，以推断2D 弹性 FWI的低频弹性数据。CNN架构通过空洞卷积获得大感受野。在Marmousi2上的实验表明从$4$ Hz 以上的带限（band-limited）数据推断出的 $2-4$ Hz 低频数据为P波和S波速度的弹性 FWI 提供了良好的初始模型。 此外，我们还研究了网络从声波数据到弹性数据的泛化能力，在弹性测试数据上， 通过弹性模拟收集训练数据集比声学模拟显示出更好的外推精度，即更小的泛化差距。

Introdcation

• 由于大部分地震数据有很强的弹性效应，仅使用声学近似不足以估计正确的反射，还会给FWI结果带来额外的假象。所以要得到高分辨率的i地球模型需要开发一种稳健的 弹性 FWI 方法。（介绍弹性 FWI的重要性）

  基础研究表明弹性 FWI 虽然能够获取地下真实属性，但在处理真实数据集方面存在一些困难。对初始模型的准确性、密度的正确估计、多参数类别的正确定义以及噪声都非常敏感。弹性波场中的复杂现象给 FWI 带来了新的挑战。（弹性 FWI上的挑战）

  在众多弹性 FWI的影响因素中，最低起始频率尤为重要，通常无法获得准确的起始模型。因为相比声波 FWI, 由于 S-波传播波长较短，EFWI 的非线性现象更为严重。因此弹性 FWI 相比 声波 FWI 总是需要较低的起始频率。此外弹性 FWI 存在参数串扰问题，且在频率较高时更为明显，因此需要超低频率才能反演 S-波速度和密度。（具体描述问题）

• 在合成数据弹性 FWI 研究中，Brossie[7]从$1.7$ Hz 开始反演Overthrust模型，Brossier[6]从$2$ Hz 开始反演Valhall模型，这两种反演都是从真实模型的高斯平滑开始，此外，Choi[10]使用$0.16$ Hz的低频速度梯度初始模型反演Marmousi2模型，Köhn等[12]在多尺度 FWI 的第一阶段使用了 $0-2$ Hz 频率。Jeong 等人[13] 从 $0.2$ Hz 开始反演同一模型。（合成数据弹性 FWI 相关研究）

  关于弹性 FWI 应用于真实数据集的报道很少。Vigh等人[16]在初始模型足够准确的情况下，将$3.5$ Hz作为弹性FWI的起始频率。Raknes等人[17]应用 3D 弹性 FWI 来更新P-波速度，并利用经验关系获得S-波速度和密度。Borisov等人[18]对一个陆地数据集进行了涉及$5-15$ Hz频段表面波的弹性 FWI。（真实数据 弹性 FWI 相关研究）

  深度学习是勘探地球物理学许多方面的新兴技术。在地震反演中，有几个研究小组已经尝试使用深度学习将数据直接映射到模型[22]-[26]。在贝叶斯地震反演框架内，深度学习已被用于制定先验[27]-[29]。其他研究小组将深度学习用作信号处理步骤，以获取用于反演的合理数据。例如，Li等人[30]使用深度学习来消除声学FWI中的弹性伪影。Siahkoohi等人[31]通过迁移学习来消除波场的数值频散。（深度学习 FWI）

• 从带限数据中通过计算外推缺失的低频是FWI缓解周期跳跃问题的最经济的方法。Li和Demanet将炮集分离为原子事件，然后改变小波以进行低频外推。Li和Demanet [34]基于扩展正演模拟的冗余性扩展频谱。Sun和Demanet [35]、Ovcharenko等人[36]以及Jin等人[37]已经利用卷积神经网络（CNN）从带限数据中外推缺失的低频。他们提出了不同的CNN架构，以从训练数据集中的不同特征学习高频和低频数据之间的映射。然而，这些研究中仅考虑了声学数据。最近，Ovcharenko等人[38]对叠前陆地数据进行了低频外推。同时，我们的初步工作[39]表明使用[40]中的深度学习模型为弹性FWI外推可靠低频的可行性。（低频外推介绍）

  尽管深度学习的机制难以解释，但低频外推的可行性已经从稀疏反演[41]和波数照明[42]的角度进行了讨论。在多道外推中，远偏移距数据的低波数作为CNN在频域中检测到的特征，用于外推缺失的低频[42]。相比之下，对于逐道外推[40]，要学习的特征是结构化的时间序列本身。逐道频率外推的可行性已经在[43]和[44]中的简单设置中通过数学证明，作为超分辨率的一个副产品。（低频外推相关研究）

  在本文中，我们将基于深度学习的外推全波形反演（EFWI）工作流程[40]扩展到弹性领域。我们使用弹性训练数据集来训练神经网络，以预测水平分量（$v_x$）和垂直分量（$v_z$）的低频数据。外推得到的低频数据用于从一个粗略的初始模型开始初始化弹性FWI。对于卷积神经网络（CNN）的架构设计，通过空洞卷积有效地实现了大感受野。此外，为了研究神经网络从声学数据到弹性数据的泛化能力，我们比较了在弹性数据和声学数据上训练的神经网络对弹性低频数据的外推结果。弹性测试数据是在深水海洋环境中的改进Marmousi2模型（称为Marmousi2）上模拟得到的，因此在这项工作中忽略了表面波。

Method

Deep Learning Models for Low-Frequency Extrapolation

• 

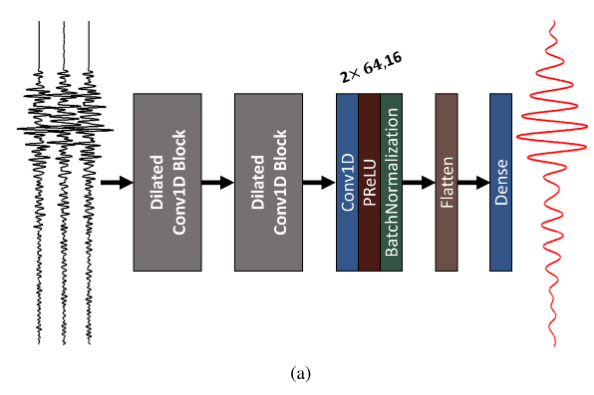
  图1. 基于空洞卷积的低频外推模型

  图1为基于空洞卷积的低频外推模型，由三条道作为输入推断中间道的低频。在这里，该架构的感受野为 1024，在对信号进行 3 倍下采样后，可以覆盖整个 1000 输入。

Training and Test Datasets

• 从3-D Overthrust模型中随机提取7个切片，其中6个切片用于训练，1个切片用于测试。每个模型大小都为$500\times 200$， 网格间距为$20$米，包括每个模型顶部的水层。每个模型顶部都有一个深度为$420$米的水层。

  图2为训练测试数据的P-波数据，其中模型的S-波数据和密度数据将根据经验公式进行计算。

  

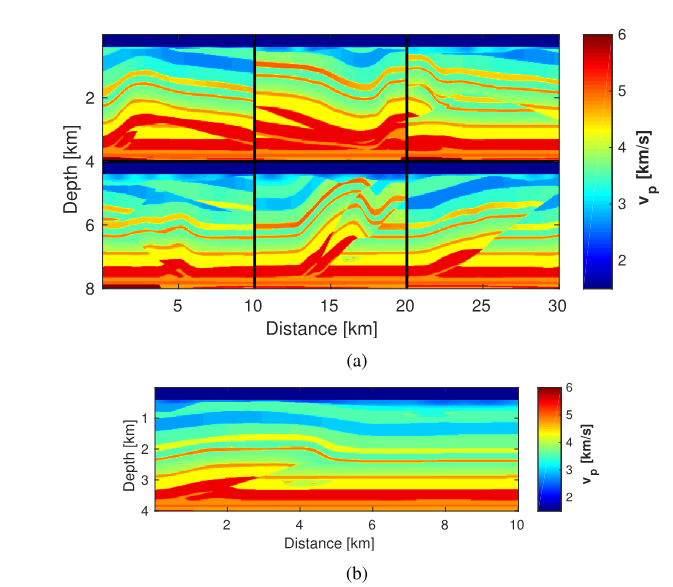
  图2. 训练数据&测试数据

  最后使用Marmousi2模型进行测试，由于训练数据和测试数据差距较大，这样可以检测网络的泛化能力。

• 正演使用2D 时域应力-速度 P-SV有限差分和八阶空间FD算子进行模拟，采用主频为$10$ Hz 的 Ricker 小波作为源信号。采样频率和记录时间分别为$0.002$和$6$ s。

  对于测试数据， 在水层 $800$ 米至 $8640$ 米处，在 $40$ 米深度均匀间隔放 $50$ 炮，在同样范围处，深度 $460$ 处，放置 $400$ 个接收器记录弹性波的$v_x$和$v_z$。

  对于训练数据，从 $500$ 米 至 $8420$ 米范围$40$深度上均匀间隔放 $100$ 炮。

  此外，每个模型顶部设置自由表面边界条件以模拟真实海洋勘探环境。自由表面会破坏低频数据，因此在模拟全波段数据中，低频波段的能量非常低。

  不同分量的数据分成两个数据集，每个训练集包含$6 \times 100 \times 398 = 238\,800$个样本，测试数据包含$1\times 50 \times 398 = 19\,900$个测试样本。

• 还对数据进行了一些预处理步骤：

  1. 归一化处理。
  2. 用常数对所有数据进行缩放。
  3. 使用平滑窗口将训练和测试数据的每个样本分离成低频信号和高频信号。
  4. 三次下采样将时间采样点数变为$1000$。

Numerical Examples

• 实验包含四个部分：

  1. 训练神经网络对Marmousi2模型低频数据进行外推。
  2. 利用外推的多分量带限低频数据为Marmousi2弹性FWI提供初始种子。
  3. 探究神经网络从声波数据到弹性数据的泛化能力。
  4. 比较本文中的架构与其他架构在低频外推上的性能。

Low-Frequency Extrapolation of Multicomponent Data

• 首先在Marmousi2上使用 $4-30$ Hz的带限数据外推 $4$ Hz以下的低频数据，使用频域平滑窗口将训练和测试u数据集的每个样本分离为 $0.125-4$ Hz 的低频信号和 $4-30$ Hz 的高频信号。

  为了处理多分量数据，神经网络需要进行两次训练：$v_x$和$v_z$。

  

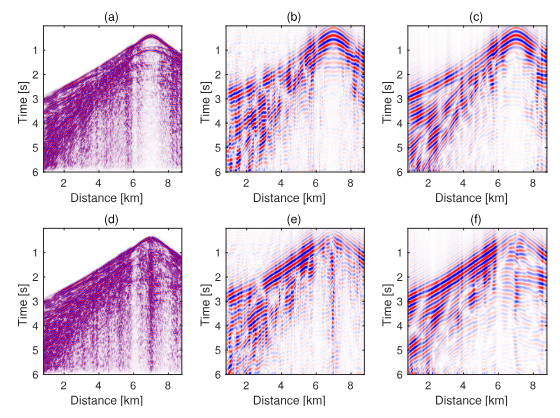
  图3. 外推结果

  图3展示了在训练在Overthrust上的网络在Marmousi2两个分量上的外推结果，震源在 $7.04$ Km处，第一列分别是$v_z$和$v_x$上的 $4-30$ Hz的带限地震记录，第二列为网络外推结果，第三列为正确的低频记录。

Extrapolated Elastic Full-Waveform Inversion

• 后续又使用了 $4-20$ Hz的带限数据对 Marmousi2 模型进行外推弹性 FWI。

  

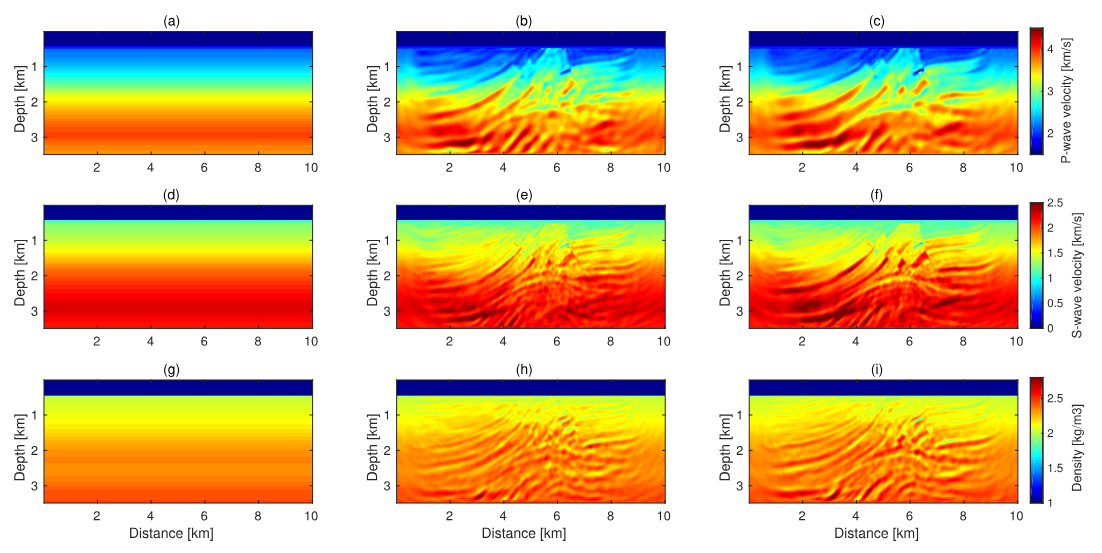
  图4. 弹性 FWI 结果

  图4展示了使用外推的低频数据作为初始模型的弹性 FWI 结果。其中图4（a）,（d）和（g）分别为$v_p,v_s$和$\rho$的初始模型，（b）和（c）分别为使用外推数据和真实 $2-4$ Hz 低频数据迭代 $30$ 次后得到的P-波速度模型。（e）和（f）分别为使用外推和真实低频数据反演的S-波速度模型。（h）和（i）分别为使用外推和真实低频数据反演的密度模型。

  可以发现外推数据反演的速度模型与真实数据反演结果几乎大致相同，而密度模型的反演并不成功，因为 $2-4$ Hz对于密度反演仍然是较高的频率。

• 然后，继续使用 $4-20$ Hz带限数据进行反演。利用多尺度方法，在弹性 FWI 中依次探索 $4-6,\ 4-10$ 和 $4-20$ Hz的频率带限数据，每个频段的迭代次数分别为 $30, 30$ 和 $20$ 次。

  

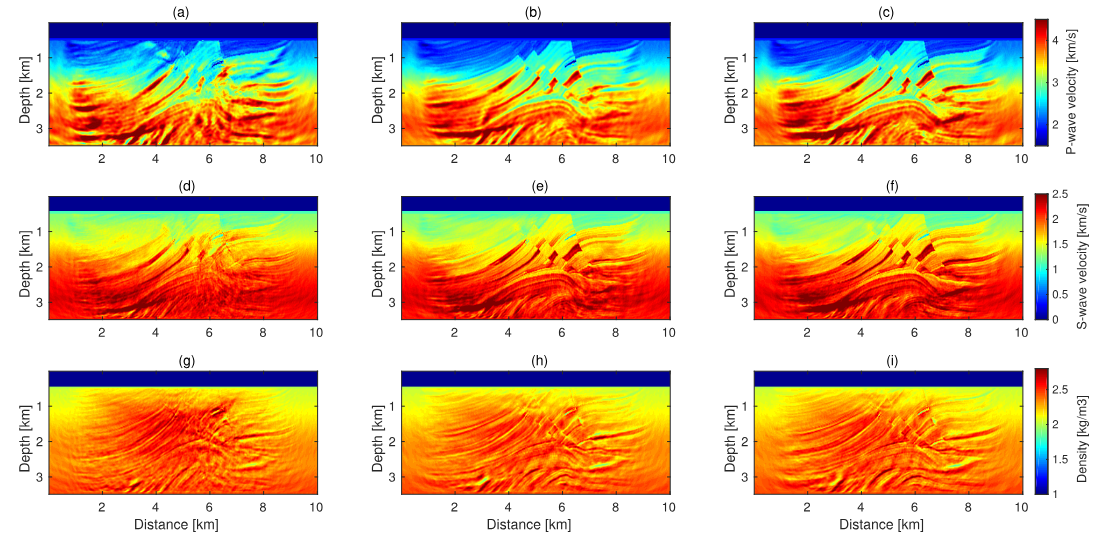
  图5. 不同低波数反演结果

  图5(a)-(f)展示了从不同低波数模型出发得到的$v_p, v_s$和$\rho$模型，（a）、（d）和（g）为使用原始初始模型开始迭代，(b)、（e）和（h）从 $2-4$ Hz外推数据反演的低波数模型开始迭代，（c）、（f）和（i）从 $2-4$ Hz真实低频数据反演的低波数模型开始迭代。

Generalization Ability of the Neural Network

• 这里研究了网络在三种情况下对于低频外推的泛化能力：不同地下结构、声学到弹性以及不同的弹性模拟代码。

  首先使用相同的弹性求解器（DENISE）模拟声学数据，将S-波数据设为零，这个例子只训练一次神经网络同时预测$v_x$和$v_z$低频。

  

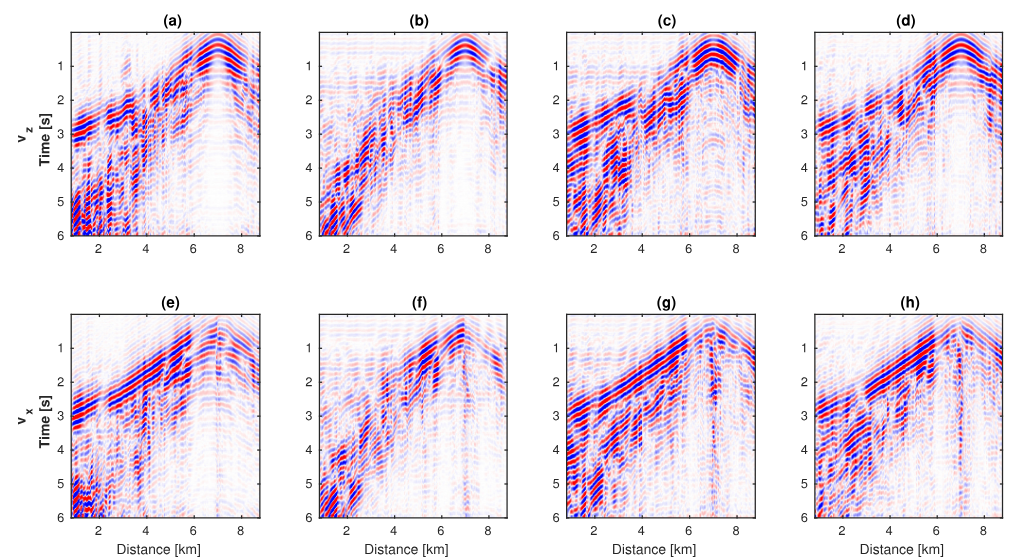
  图6. 不同训练参数低频外推结果

  图6比较了使用声学$v_z$、仅使用弹性$v_z$、仅使用弹性$v_x$以及同时使用弹性$v_x$和$v_z$训练的升级网络推断出的位于 $7.04$ Km处的 $0.125-4$ Hz低频。与同时弹性$v_x$和$v_z$分量进行训练相比，使用声学数据或弹性数据单一分量进行训练会降低外推低频的精度。

• 后续作者又使用“fdelmodc”模拟声学或弹性训练数据集，使用“DENISE”模拟弹性测试数据集。声学训练数据集使用 2D 可变密度声波方程对弹性模拟中使用的P-波速度模型和相关密度模型进行正演模拟。

  

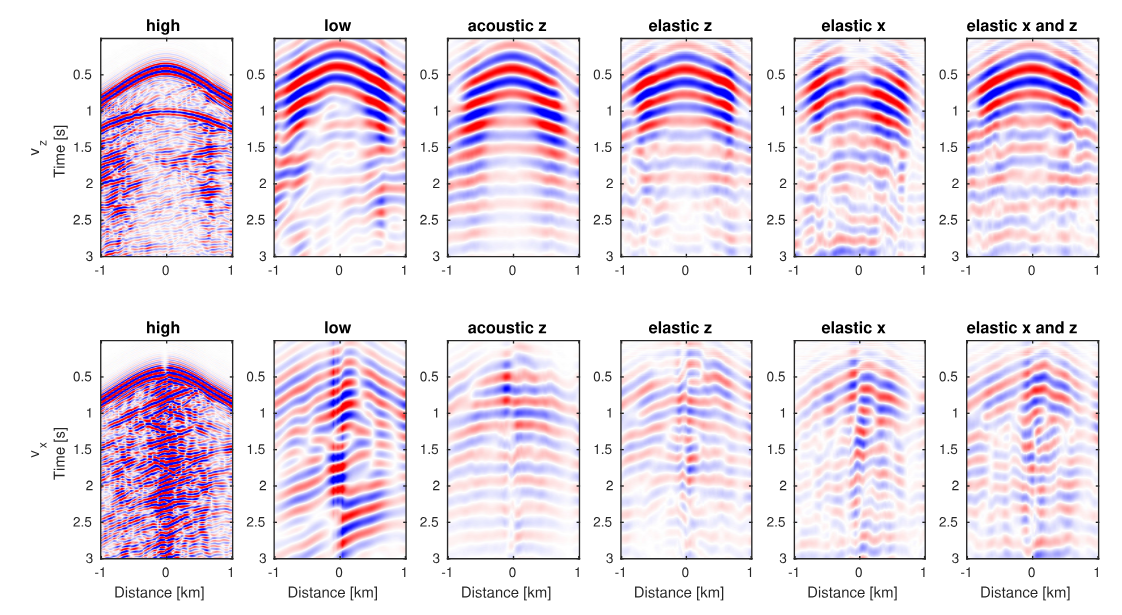
  图7. 不同程序正演数据外推结果

  从图7可以看出使用弹性$v_x$进行训练也无法恢复零偏移（震源）附近事件的连续性，相反使用弹性$v_z$和$v_x$进行训练可使神经网络恢复弹性$v_x$的P-S极性反转效应（P-S polarity reversal effect）和弹性$v_z$的近零偏时间连续性。实验表明使用不同求解器模拟训练数据和测试数据时， 从声学数据到弹性数据的泛化差距会变大。

  最后对比了不同网络的性能，另一个网络为作者之前的工作，没有使用空洞卷积。

Discussion and Limitations

Physical Interpretation

Is the problem at all solvable?

• 为什么神经网络可以用于解决带宽外推问题？作者认为在以下情况下，外推带宽是有利的：

  1. 波是脉冲的
  2. 波传播的介质是非惰性的

  这种情况作者认为改变波的频率内容就是识别孤立波并改变时间特征，同时保持到达时间不变。此设置与更改语言音调非常相似。

Is the problem necessarily hard?

• 一般来说，外推频率是一个难以解决的问题，但如上所述，在某些（理想）情况下，频率外推也是一个可解决问题，一般u来说哦，将脉冲波的频率含量从高到低改变会产生干扰，无论是建设性干扰还是破坏性干扰，因为波的足迹变大了。

  这没问题，但是一般将低频改为高频可能会更难，因为这需要消除这种干扰，在本文中，我们并不试图产生无法观察到的高频。

Dose a neural network know the right physics to compute low frequencies?

• 神经网络是作为通用近似器构造的，本文中神经网络不需要利用物理原理来“增强”其工作能力——只要训练集能够代表物理信息即可。目前还不知道神经网络执行了什么操作取得成功，但这是未来的一个重要研究课题。

Might a neural network even have the capability to perform frequency extrapolation?

• 除了作为通用近似器外，神经网络还可以执行频率外推所需的非线性信号处理，例如一个简单的使用ReLU激活函数的浅层神经网络可以轻松实现：

  1. 提取高频波形，去除其负部分。这会产生$\omega = 0$的低频。
  2. 用一个适当滤波器进行卷积，用低频小波代替高频小波正向部分。

  虽然两种操作不能提供准确的预测结果，但它们表明e神经网络可能需要的操作类型。

Limitations and Variations

• 使用FWI恢复密度非常困难，这与带宽外推无关，因为

  1. 使用短偏移数据会产生串扰，因为P-波速度和密度在短孔径处具有相同的辐射模式；
  2. 密度的变化小于速度变化；
  3. 密度反演需要超低频率。

  虽然弹性 FWI 并不能完全正确估计密度，但它更可能利用外推或真实低频重建速度。

• 在 EFWI 中，起始频率的选择需要在外推法低频数据的准确性与缓解周期跳跃问题的最低频率之间权衡，由于近零频率范围内的外推精度不够，作者使用 $2-4$ Hz的外推低频数据作为起始评论。从 $4$ Hz 带限数据开始， $2-4$ Hz的外推低频数据的精确度足够以对P-波和S-波速度进行弹性 FWI。

  但是对于密度反演， $2-4$ Hz的外推低频数据的精确度不足以进行密度反演， 因此反演的密度模型缺乏低波数结构。

Future Work on the Application to Field Data

• 本文的想法是应用于实地数据缺乏低频数据，即数据是无标签的。后续工作有

  1. 利用反演模型的先验知识建立训练模型，例如事先估计了水底深度，则可用相同水底深度建立训练模型。
  2. 由于实地数据与模拟数据之间存在振幅差异，应使用与合成数据相同的方式对带限数据进行归一化。如果 FWI 使用的是对振幅不敏感的代价函数，则无需恢复现场数据的原始振幅。
  3. 本文假定外推弹性 FWI 的源信号已知，然而现场数据的源信号可能随着炮点改变而改变，因此可以先检索现场数据集的源小波，然后去噪人为提高低频能量。新的源信号可以用于合成低频外推的训练数据集。它还可以成为后续使用外推低频数据进行 FWI 的源小波。通过这种方式，可以在一定程度上控制源的不确定性。

总结

1. 一个基于空洞卷积的CNN网络进行低频外推。
2. 将波分为两个正交分量进行训练和预测。
3. 探究了网络对于声波和弹性波的泛化能力。