禁忌搜索算法
禁忌搜索算法
解决什么问题
启发式搜索算法——求解近似值
解决无法找到精确解的复杂优化问题,例如背包问题、神经网络训练、调度问题、工程设计问题。(引入)
特点是利用过去的经验解决具体问题。 有时候不能保证问题一定结局,却常常能有效解决问题。
分类
基于群体
每次迭代搜索一组解,算法依赖于多个个体之间的信息交互。
基于个体
关注单个解,从某个解出发迭代得到最优解。
核心思想
给出多个迭代方向、逃离局部最优解
各类最优化问题的搜索方案
爬山算法
从当前节点开始和邻节点进行比较,不断向最大值移动。
贪心策略,简单但很显然容易陷入局部最优。
模拟退火
以一定概率接受比当前解差的邻居解,概率会随着时间增加(或者说温度下降)而降低。
工程方面广泛应用,但还是可能陷入局部最优。
禁忌搜索
模拟人的经验,通过禁忌表记录最近搜索的历史信息,排除某些解。
禁忌搜索
通过引入一个灵活的存储结构和相应的禁忌准则来避免暂时的重复搜索。
一个例子,一日三餐,为了寻找最好的搭配。
当10月1日(初始日)中午随机选了几样东西作为食物,早上:面包,中午:米饭,晚上:面条; 当10月2日(第二次迭代),在众多相近的选择中(邻居解集合),我选择效果最好的,早上:面包,中午:面条,晚上:面条, 2日整体效果比1日好,那么其变化为:中午由 米饭->面条, “中午:米饭”这个属性被我记住了(禁忌表),在接下来几天(禁忌长度)中,对于邻居解中任何有“中午:米饭”的解,我将不会考虑,除非该解比历史最好的效果都好(解禁条件)。
引出两个概念
- 禁忌表:记录被禁止的属性,其值为禁忌长度,该长度范围内,该属性被禁止。
- 解禁条件:当含有禁忌属性的解,效果好于历史最好解时,我们选择这个被禁忌的解,其他情况,被禁忌的解不予考虑。
伪代码
\begin{algorithm} \caption{禁忌搜索算法伪代码} \begin{algorithmic} \STATE \textbf{输入:} 初始解$x_0$,禁忌表大小$T_{size}$,最大迭代次数$max\_iter$,邻域生成函数$NeighborGen$,目标函数$Objective$,禁忌长度$tabu\_tenure$ \STATE \textbf{输出:} 最优解 $X_{sol}$,最优值 $X_{v}$ \STATE 初始化 $X_{sol} \leftarrow x_0$,$X_v \leftarrow Objective(x_0)$ \STATE 初始化禁忌表 $TabuList \leftarrow \emptyset$ \PROCEDURE{Tabusearch}{} \FOR{$iter = 1$ to $max\_iter$} \STATE 当前解 $current\_solution \leftarrow best\_solution$ \STATE 生成当前解的邻域 $Neighbors \leftarrow NeighborGen(current\_solution)$ \STATE 初始化最优邻域解 $best\_neighbor \leftarrow \emptyset$,$best\_neighbor\_value \leftarrow \infty$ \FOR{每个邻域解 $neighbor$ in $Neighbors$} \IF{$neighbor$ 不在 $TabuList$ 或 $neighbor$ 的禁忌时间已过} \STATE 计算邻域解的目标值 $neighbor\_value \leftarrow Objective(neighbor)$ \IF{$neighbor\_value < best\_neighbor\_value$} \STATE 更新最优邻域解 $best\_neighbor \leftarrow neighbor$,$best\_neighbor\_value \leftarrow neighbor\_value$ \ENDIF \ENDIF \ENDFOR \IF{$best\_neighbor\_value < best\_value$} \STATE 更新最优解 $best\_solution \leftarrow best\_neighbor$,$best\_value \leftarrow best\_neighbor\_value$ \ENDIF \STATE 将 $current\_solution$ 或其特定属性加入 $TabuList$,设置禁忌时间 $tabu\_tenure$ \STATE 更新禁忌表,移除已过禁忌时间的解 \ENDFOR \ENDPROCEDURE \end{algorithmic} \end{algorithm}
应用
图染色问题
给定一个无向图,其中为顶点集合,为边集合,图染色问题是将每个顶点涂上颜色,使得每个相邻的顶点着不同的颜色,求出最少使用的颜色数K。
这个问题可以归约为对于一个颜色数是否存在某种染色方案使相邻两节点颜色不同(-着色问题)。此时我们可以不断减少得到最初问题的解。
重写为数学语言即对于集合,其中代表颜色为的顶点的集合。显然若所有为独立集,则为合法解,否则为冲突解。
定义目标函数为冲突数
其中
对于所有的合法解。
局部搜索
对于局部搜索法,可以通过下列步骤求解上述问题
初始化解:为每个顶点从到随机选取一个颜色(也可以通过某种启发式策略产生初始解,但一个好的算法不应对初始解敏感)。
定义领域动作:对于每个产生冲突的顶点,令其颜色等于其它个颜色,领域大小等于冲突顶点数乘以。
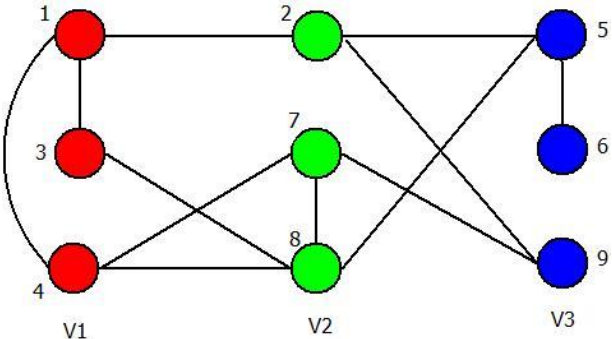
图1. 示例 例如对于图1,的情况。冲突对为,冲突边为条,则,领域大小为。
定义邻色表,代表当顶点为颜色时对应的冲突数。
图1的邻色表为
定义动作
move(u,i,j)代表将顶点颜色从变为,定义残差值,显然目标函数值将变为。更新邻色表,更新原则为:对于
move(u,i,j),更新顶点的行,第列减一,第列加一。
显然局部搜索只关系每个顶点相连接的邻节点,通过不断更新颜色获得最佳方案(最小的值)使得获得一个解。
禁忌搜索
在禁忌搜索中,我们引入禁忌表使执行
move(u,i,j)后,顶点在接下来的次迭代中禁止回到颜色。禁忌表为
TabuTenure[N][K],其中TabuTenure[u][i]存储一个迭代次数,代表顶点在该次数之前禁止回到颜色。同时,我们在迭代中还需要判断每个邻居解的质量,若其为禁忌解但是当前最好解且优于历史最好解,则进行解禁操作。
