现代密码学

• 2024研究生课程「现代密码学」笔记&复习要点。

现代密码学关注的安全属性和攻击方式

安全属性

• 信息安全关注CIA，密码学安全关注五要素

1. 保密性（Confidentiality）：保证信息被授权者使用而不泄露给未授权者。即授权者无法获取明文；
2. 完整性（Integrity）：数据完整：数据不被未授权篡改或损坏。系统完整：系统不被未授权操控；
3. 可用性（Availability）：保证信息和系统随机对授权者可用，不应出现对授权者拒绝或被未授权者滥用；
4. 认证性（Authenticity）：消息认证：认证消息来源和消息完整性。身份认证：保证通信实体真实性；
5. 不可否认性（Non-repudiation）：发送接受双方不能否认已传输完成的消息。

• 密码分为密码编码学和密码分析学。
• 柯克霍夫准则：密码系统的安全性不应依赖其系统的保密性（即使算法公开，只要密钥未泄露，它就该是安全的）

攻击方式

1. 按照可获得的信息进行分类

   1. 唯密文攻击（仅知道一些密文）
   2. 已知明文攻击（知道一些明密文对）
   3. 选择明文攻击（可以选择明文得到密文）
   4. 选择密文攻击（可以选择密文得到明文）
   5. 选择文本攻击

2. 按照攻击方式进行分类

   1. 穷举攻击（防御：增大密钥量）
   2. 统计分析攻击（防御：使明文和密文统计特性不一样）
   3. 数学分析攻击（防御：使用足够复杂的加密算法）

安全性

1. 无条件安全性：绝对安全，例如一次一密。
2. 计算安全性：已知的最好破解方法所需代价超过了破译者的能力（时间、空间、资源等）
3. 可证明安全性

Hill密码的加密解密过程

加密

1. 随机生成或选择一个可逆的密钥矩阵$\mathbf{B}$。
2. 将明文分为三个字母一组，不足用"X"代替，并转化为数字（A=0, B=1, ...）。
3. 将数字组与密钥相乘再转为字母，拼接得到密文串。

解密

1. 求出密钥矩阵的逆矩阵。
2. 将字母转为数字进行相乘，得到明文。

分组密码工作模式

ECB（电子密码本）

ECB加密

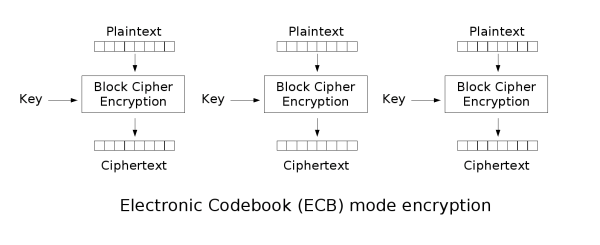
• 优点：加密速度块。

  缺点：相同的明文得到相同的密文，不会隐藏明文分组的统计规律，可能存在替换攻击。

CBC（密码分组链接）

CBC加密

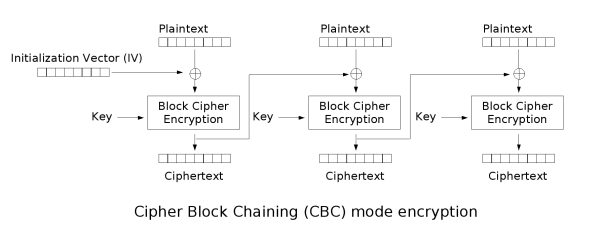
• 优点：

  1. 密文块不仅和当前密文块相关，而且和前一个密文块或 IV 相关，隐藏了明文的统计特性。
  2. 具有有限的两步错误传播特性，即密文块中的一位变化只会影响当前密文块和下一密文块。
  3. 具有自同步特性，即第$k$块起密文正确，则第$k+1$块就能正常解密。

  缺点：加密不能并行，解密可以并行。

CFB（密文反馈）

alt text

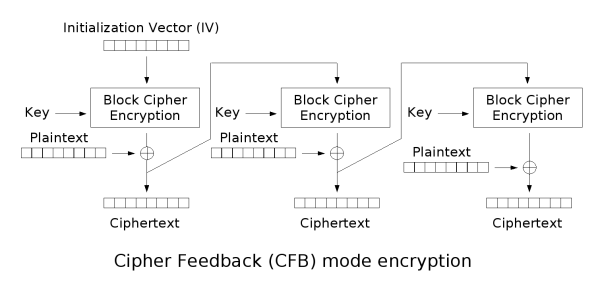
• 优点：

  1. 适应不同数据格式的要求
  2. 有限错误传播
  3. 自同步特性

  缺点：加密不能并行化，解密不能并行

OFB（输出反馈）

alt text

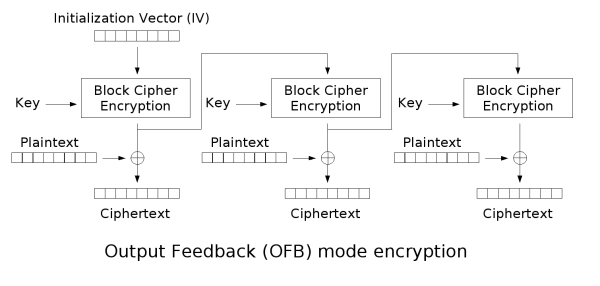
• 优点：不具有错误传播特性

  缺点：在信号易出错且冗余较多的环境下可能需要额外的错误处理机制。

CTR（计数器）

alt text

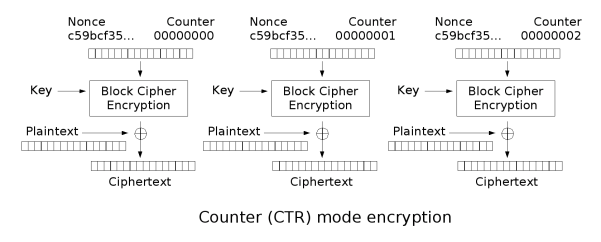
• 优点：高效且支持随机访问；支持并行加密；简单且安全

  缺点：如果计数器被重用，则可能有安全漏洞。

Hash函数的安全属性和应用示例

安全属性

1. 单向性：给定一个哈希值，很难找到对应原始输入。
2. 抗弱碰撞性：很难找到两个不同输入产生相同的哈希。
3. 抗强碰撞性：对于任意给定输入，很难找到不同的输入产生相同的哈希。

应用

1. 隐私信息存储，用户密码加密存储；
2. 消息签名认证，对参数计算哈希防篡改；
3. 完整性校验，保证数据完整性；

RSA在公钥加密/数字签名中的运算

RSA加解密

• 密钥生成

  1. 选择大素数$p,q$，计算$n = p\times q$；
  2. 选择$e \in [1, n]$，满足$(e, n) = 1$；
  3. 计算$e$在模$\varphi(n)$下的逆元$d$，满足$ed\equiv 1 \pmod{\varphi(n)}$；

  $(e,n)$为公钥，$(d, n)$为私钥。

• 加密

  对明文$m$进行加密$c = m^e \bmod{n}$。

• 解密

  $m = c^d \bmod{n}$

数字签名

• 使用私钥加密消息

  $s = m^d \bmod{n}$

  验证签名：$m = s^e \bmod{n}$。

密钥配送问题的两种密钥建立方式（对称的，公钥的）

• Q：如何在不可信的信道中建立安全通信环境？

  A：使用加密算法对消息进行加密，但如何交换/传递加密算法所使用的密钥本身也是一个问题。

对称密钥建立

1. 实现约定/共享

   事先以安全的方式交换密钥

   缺点：

   1. 物理上不可行（例如双方异地）；
   2. 两两通信需要一个密钥，存储密钥数量过多（$n$个人需要$n(n-1)/2$个密钥）；

2. 密钥分配中心

   需要加密时，分配中心生成一个通信密钥，每个人只需要事先和密钥分配中心共享密钥即可。

   缺点：存在单点故障风险，KDC故障整个网络都将被破坏。

公钥密码建立

1. Diffie-Hellman密钥交换

   1. A和B共同选择一个素数$p$和本原根$g$，有$2\le g \le p-1$。
   2. A产生一个私有随机数$k_a \in [1,p-1]$，计算$y_a \equiv g^{k_a} \pmod{p}$，发送给B。
   3. B产生一个私有随机数$k_b \in [1,p-1]$，计算$y_b \equiv g^{k_b} \pmod{p}$，发送给A。
   4. A计算$K = y_b^{k_a}$得到密钥，同理B计算$K = y_a^{k_b}$得到密钥。易知二者相等。

   缺陷：

   1. 如果网络存在主动攻击者M，可以拦截$y_a,y_b$并生成$g^s$发送给A和B。此时M便可以解密通信密文并且伪造A或B发送消息。

2. 其他公钥密码

   直接使用对方的公开公钥加密消息进行传输。

ECC倍点运算

• 对于椭圆曲线$E: y^2 = x^3 + ax + b$，设$P(x_1,y_1),Q(x_2,y_2)$为$E$上两点，当$P\not = \pm Q$时，有$P+Q = (x_3,y_3)$，其中

  $$\begin{aligned} s &= \frac{y_2 - y_1}{x_2-x_1}\\ x_3 &= s^2 - x_1 - x_2\\ y_3 &= s(x_1 - x_3) - y_1 \end{aligned}$$

  当$P=-Q$时，$P+Q = O$，当$P=Q$时，$P+Q = 2P = (x_3,y_3)$，其中

  $$\begin{aligned} s &= \frac{3x_1^2 + a}{2y_1}\\ x_3 &= s^2 - 2x_1\\ y_3 &= s(x_1 - x_3) - y_1 \end{aligned}$$

  

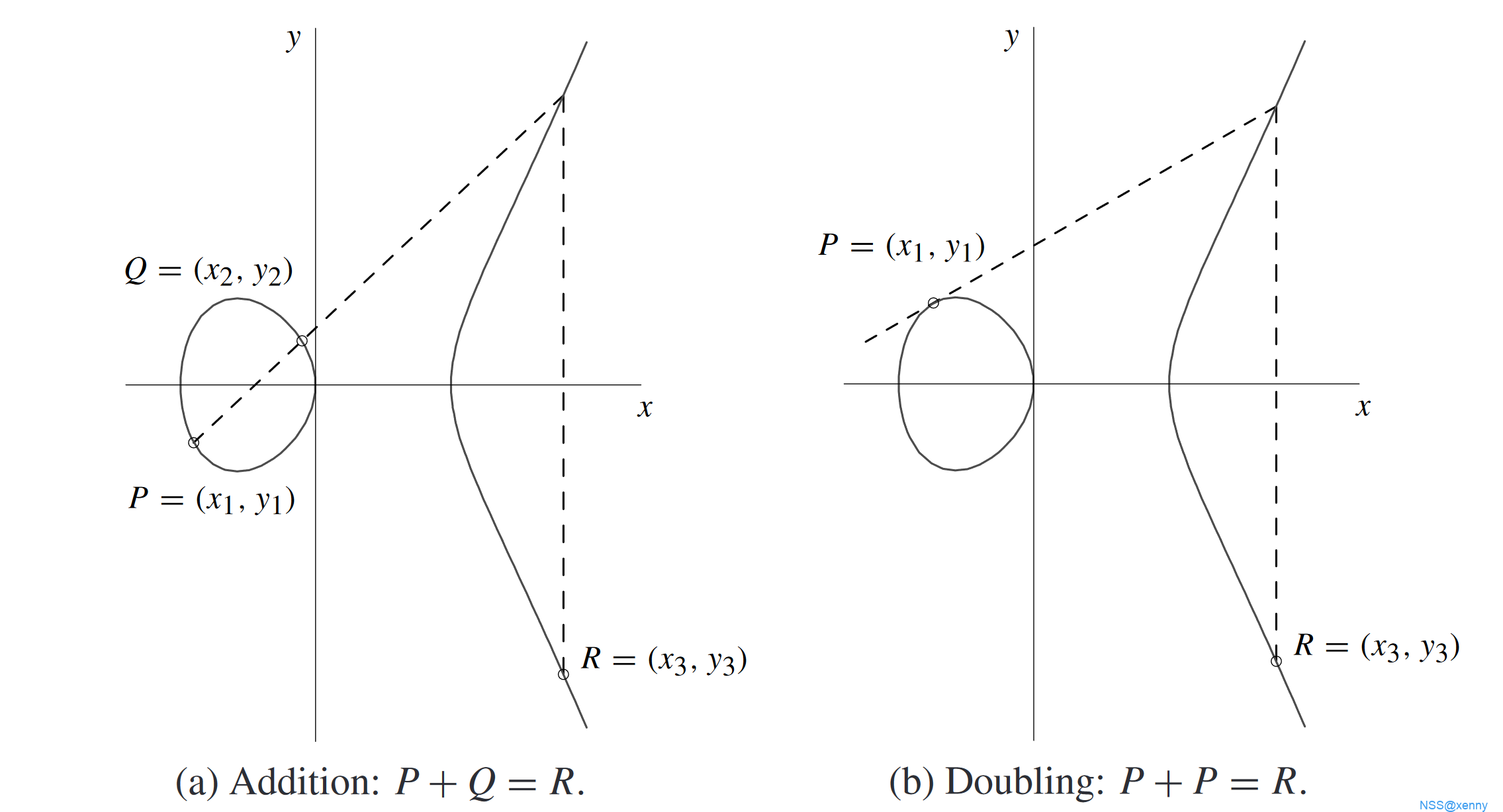
  椭圆曲线运算

  本质就是两点连线与$E$的交点关于$x$轴的对称点。公式还是比较好记的，$s$就是代表斜率，有两点则用两点式求，一点则直接对原方程求导得到。

Shamir门限方案的秘密恢复计算

• Shamir门限方案是一种秘密共享方案，它允许将一个秘密分割成多个份额，并将这些份额分发给不同的参与者。只有当足够数量的参与者合作时，才能恢复出原始的秘密。

  本质就是离散插值，原函数是$t-1$阶函数，生成$n$个$(x, y)$坐标至少使用$t$个坐标便能通过插值恢复原函数。

秘密分割

• 对于秘密$S$，选择一个$t-1$阶多项式函数$f(x)$表示秘密

  $$f(x) \equiv S + a_1x + a_2x^2 + \cdots + a_{t-1}x^{t-1} \pmod{p}$$

  选择多个不同的$x_i$值，计算对应的$f(x_i)$作为份额进行分发。

秘密恢复

• 计算拉格朗日插值函数

  $$P(x) \equiv \sum_{i}^{t-1} y_i \prod_{j,j\not = i}^{t-1}{\frac{(x-x_j)}{(x_i-x_j)}} \pmod{p}$$

  然后计算$P(0)$即可恢复秘密$S$。