数值分析

• 2024研究生课程「数值分析」笔记&复习要点。

1. 绪论

1.1. 误差和误差限

1. 绝对误差

   $$e^{*} = x^{*} - x$$

   即真实值和近似值的绝对差，一般情况我们不知道真实值，所以求不出绝对误差。但是可以求绝对误差限$\vert e^{*}\vert < \varepsilon$。

2. 相对误差

   $$e^{*}_r \approx \frac{e^{*}}{x^{*}} = \frac{x^{*} - x}{x^{*}}$$

   相对误差限为$\vert e^{*}_r\vert < \varepsilon_r$。

1.2. 有效数字

• 若$\vert e^{*}\vert \le \frac{1}{2}\times 10^{m-n}$，且$x^{*} = \pm 0.a_1a_2a_3\dots a_n \times10^{m}$，则$x^{*}$有$n$位有效数值。

  这里说人话就是把数先变成科学计数法，然后再看$\le \frac{1}{2}\times 10^{k}$，$k$就是有效位数。

  例如$3.142$作为$\pi$近似时的有效数字：

  $$\begin{aligned} \vert \pi - 3.142\vert &= 0.0004073\dots\\ &\le 0.0005\\ &= \frac{1}{2}\times 10^{-3} \end{aligned}$$

  且$\pi = 0.314\dots \times 10^1, 3.142 = 0.3142 \times 10^1$，所以$m-n = -3$得$n=4$，即有$4$位有效数字。

  若$x^{*}$有$n$位误差，则$x^{*}$的相对误差限满足

  $$\vert e^{*}_r \vert \le \frac{1}{2a_1} \times 10^{1-n}$$

• 数值计算

  1. 不要扩大误差，例如迭代解乘上常数$kx_n = x_{n+1}+\dots$改为$x_n = \frac{1}{n}(x_{n+1} + \dots)$。
  2. 不要近似数减法，一般做有理化处理。
  3. 绝对值太小不做分母
  4. 大数不要减小数
  5. 简化算法。

2. 插值

2.1. 概念

• $n+1$个点的插值函数存在且唯一。

• 线性插值

  即两个点插值，参考拉格朗日$n=1$情况。

• 二次/抛物线插值

  三个点插值，设插值函数为$L_2(x) = a_0x^2 + a_1x + a_2$，然后带入求解即可。

2.2. 拉格朗日插值

• 插值多项式为

  $$L_n(x) = y_0l_0(x) + y_1l_1(x) + \cdots + y_nl_n(x)$$

  满足$L_n(x_k) = y_k$，其中插值基函数$l_i(x)$为

  $$l_i(x) = \frac{(x-x_0)(x-x_1)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x - x_n)}{(x_i-x_0)(x_i-x_1)\cdots(x_i-x_{i-1})(x_i-x_{i+1})\cdots(x_i - x_n)}$$

  插值余项为

  $$R_n(x) = f(x) - L_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}\omega_{n+1}(x),\quad \xi \in (a,b),\ \omega_{n+1}(x) = \prod_{i=0}^n(x-x_i)$$

2.3. 牛顿插值

• 是一种迭代插值方式，可以复用之前的计算内容，插值多项式为

  $$N_n(x) = N_{n-1}(x) + a_n(x-x_0)(x-x_1)\cdots(x-x_{n-1})$$

1. 差商

   • 一阶差商（均差）

     $$f[x_0,x_k] = \frac{f(x_k) - f(x_0)}{x_k-x_0}$$

   • $k$阶差商

     $$f[x_0,x_1,\dots,x_k] = \frac{f[x_0,x_1,\cdots,x_{k-1},x_k]-f[x_0,x_1,\cdots,x_{k-1}]}{x_k-x_{k-1}}$$

   $n$阶差商和$n$阶导数关系$f[x_0,x_1,\cdots,x_n] = \frac{f^{(n)}(\xi)}{n!},\quad \xi\in[a,b]$。

   计算的时候写成差商表。记住分母就是分子里是$x_k$分母就是$x_k$。

• 回到牛顿插值，其系数$a_i$则等于$f[x_0,\dots,x_i]$，最终插值多项式为

  $$N_n(x) = f(x_0)+f[x_0,x_1](x-x_0) + f[x_0,\dots,x_2](x-x_0)(x-x_1) + \cdots,$$

  其插值余项为

  $$R(x) = f[x_0,x_1,\dots,x_n](x-x_0)\cdots(x-x_n)$$

2.4. 牛顿等距插值

• 差分

  已知等距节点$x_k = x_0 + kh,\quad k=0,1,\dots,n,\quad h=\frac{x_n-x_0}{n}$。

  记向前差分/前差算子为

  $$\Delta f(x_k) = f(x_{k+1}) - f(x_k)$$

  向后差分/后差算子为

  $$\nabla f(x_k) = f(x_k) - f(x_{k-1})$$

  中心差分为

  $$\delta f(x_k) = f(x_k+\frac{h}{2}) - f(x_k - \frac{h}{2})$$

• 高阶差分

  规定零阶差分：$\Delta^0 f_i = \nabla^0 f_i = f_i$。

  $m$阶差分为$\Delta^m f_k = \Delta^{m-1}f_{k+1} - \Delta^{m-1}f_k$，其他同理。

  和差商关系

  $$f[x_k,x_{k+1}] = \frac{\Delta f_k}{h}$$

  $$f[x_k,x_{k+1},\dots,x_{k+m}] = \frac{1}{m!}\frac{1}{h^m}\Delta^m f_k$$

  计算时写差分表，倒三角矩阵。

• 此时可得牛顿等距插值多项式为

  $$N_n(x_0+th) = f_0 + t\Delta f_0 + \dots + \frac{t(t-1)\cdots(t-n+1)}{n!}\Delta^n f_0$$

2.5. Hermite插值

• 当知道$\{y_n=f(x_n)\}$和一阶导数$\{m_n=f'(x_n)\}$时使用。

  对于$n$阶插值式，有$2n+2$个已知数，此时令$\alpha_j(x),\beta_j(x)$为$2n+1$次多项式，且满足

  $$\begin{cases} \alpha_j(x_k) = \delta_{jk},\\ \alpha_j'(x_k) = 0. \end{cases}\quad \begin{cases} \beta_j(x_k) = 0,\\ \beta_j'(x_k) = \delta_{jk}. \end{cases}$$

  其中

  $$\delta_{jk} = \begin{cases} 0,\quad j\not = k,\\ 1,\quad j=k \end{cases}$$

  为克罗内克（Kronecker）符号。 则有$H(x) = \sum_{j=0}^n \alpha_j(x)y_j + \beta_j(x)m_j$。

  令$\alpha_j(x) = (ax+b)l_j^2(x)$，显然有$ax_j + b = 1$。

  且$\alpha_j'(x) = al_j^2(x)+2(ax+b)l_j(x)l_j'(x)$，有$a+2(ax_j+b)l_j'(x_j)=0$。

  联立解得

  $$\begin{aligned} \alpha_j(x) &= [1-2(x-x_j)l_j'(x_j)]l_j^2(x) \\ &= \left[1-2(x-x_j)\sum_{\begin{subarray}{l} k=0\\ k\not =j \end{subarray}}^{n}{\frac{1}{x_j-x_k}}\right]l_j^2(x). \end{aligned}$$

  令$\beta_j(x) = (cx+d)l_j^2(x)$，同理可得

  $$\beta_j(x) = (x-x_j)l_j^2(x).$$

3. 曲线拟合

3.1. 函数逼近

1. 最佳一致逼近

   即MAE最小

2. 最佳平方逼近

   取$\sqrt{\int_a^b{[f(x)-P(x)]^2}\mathrm{d}x} = \lVert f(x)-P(x)\rVert_2$。

   对于线性空间

   $$\Phi = \mathrm{span}\{\varphi_0,\varphi_1,\dots,\varphi_n\}.$$

   称$\{\varphi_i(x)\}$为生成集合$\Phi$的一个基底。

• 解题时则对应不同得空间定义

  $$g(x) = a_0\varphi_0 + a_1\varphi_1 + \dots,$$

  然后目标是最小化$I = \int_a^b{[f(x)-P(x)]^2}\mathrm{d}x$。

  则利用$\frac{\partial I}{\partial a_k} = 0$列方程组，即可解出$\{a_i\}$得到$g(x)$。

• 矩阵形式求解则先求内积

  $$(\varphi_i, f) = \int_a^b{\varphi_i\cdot f}\mathrm{d}x$$

  然后有

  $$\begin{bmatrix} 1&1/2&1/3&\cdots\\ 1/2&1/3&1/4&\cdots\\ \vdots&\vdots&\vdots&\vdots\\ 1/n&1/(n+1)&1/(2n+1)&\cdots\\ \end{bmatrix}\begin{pmatrix} a_0\\ a_1\\ a_2\\ \vdots\\ a_n \end{pmatrix} = \begin{pmatrix} (\varphi_0, f)\\ (\varphi_1, f)\\ (\varphi_2, f)\\ \vdots\\ (\varphi_n, f) \end{pmatrix}$$

3.2. 最小二乘法

• 相当于是散点函数拟合，只是一些算子计算方式变了，思路同上。对于$\{x_i\}$和$\{y_i\}$，我们同样也是找拟合，具体做法为

  设$y^{*}(x) = a_0\varphi_0 + \dots,$为拟合函数，基函数为$\varphi_0(x)=1, \dots$，有

  $$\begin{bmatrix} (\varphi_0,\varphi_0)&(\varphi_0,\varphi_1)&\cdots\\ (\varphi_1,\varphi_0)&(\varphi_1,\varphi_1)&\cdots\\ \vdots&\vdots&\vdots\\ (\varphi_n,\varphi_0)&(\varphi_n,\varphi_1)&\cdots\\ \end{bmatrix}\begin{pmatrix} a_0\\ a_1\\ \vdots\\ a_n \end{pmatrix} = \begin{pmatrix} (\varphi_0, f)\\ (\varphi_1, f)\\ \vdots\\ (\varphi_n, f) \end{pmatrix}$$

  （内积为$(\varphi_j, \varphi_k) = \sum_{i=0}^n{\varphi_j(x_i)\varphi_k(x_i)}$）

  解出$\{a_i\}$后，即得到拟合函数$y^{*}(x) = \dots$，其对应的平方误差为

  $$\lVert \delta^{*} \rVert_2^2 = \sum_{i=0}^n(y^{*}(x_i) - y_i)^2$$

4. 数值积分

4.1. 插值求积公式

• 梯形公式：$\int_a^b f(x)\mathrm{d}x \approx \frac{1}{2}(b-a)[f(a)+f(b)]$

  把区间分成两份。

• 辛普森公式：$\int_a^b\mathrm{d}x \approx \frac{1}{6}(b-a)[f(a)+4f(\frac{a+b}{2})+f(b)]$

  把区间分成六份。误差：$R_2(f) = -\frac{(b-a)^5}{2880}f^{(4)}(\eta),\quad \eta\in (a,b)$。

• 对于任意插值多项式$p(x) = \sum_{k=0}^n{f(x_k)l_k(x)}$，有效数字

  $$\begin{aligned} \sum_a^b{f(x)}\mathrm{d}x &\approx \int_a^b P(x)\mathrm{d}x \\ &= \sum_{k=0}^n f(x_k)\int_a^b l_k(x)\mathrm{d}x \\ &= \sum_{k=0}^n f(x_k)A_k \end{aligned}$$

  其中求积系数和$\sum A_k = (b-a)$，其求积余项$R(f) = \int_a^b[f(x) - P(x)]\mathrm{d}x = \int_a^b \frac{f^{(n+1)}(\xi)}{(n+1)!}\omega(x)\mathrm{d}x$。

• 代数精度：对于$m$阶多项式准确且对于$m+1$阶不准确则代数精度为$m$。

  已知公式求精度解题时则分别取$f(x) = 1, x, x^2, \dots$，带入$\int_a^b f(x)\mathrm{d}x = \int_a^b P(x) \mathrm{d}x$等式两侧。

  找到不相等得阶数得到代数精度。

  具有$n+1$个节点的插值求积公式至少有$n$次代数精度，反过来如果不符合这个则说明公式不是插值型的。

  已知精度求等式时也一样，分别取$f(x) = 1, x, x^2, \dots$，带入等式两侧获得方程组求解待定系数。

4.2. 收敛性&稳定性

• 不在复习范围。

4.3. 牛顿-柯斯特求积公式

• 不在复习范围。知道这个公式是上述各个公式的通项即可。

4.4. 复化求积公式

• 求积节点增加，直接使用牛-柯求积公式会放大误差。所以采用分区间分别求积的方式。

• 复化梯形

  将区间$[a,b]$分为$n$份，步长$h=\frac{b-a}{n}$，求积节点为$x_k=a+kh,\ (k=0,1,\dots)$。

  有

  $$T_n = \frac{h}{2}\left[f(a) +2\sum_{k=1}^{n-1}f(x_k)+f(b)\right].$$

  推导即对每个小区间分别使用梯形再加起来即可，过程略。其求积余项/误差为

  $$R_T = -\frac{b-a}{12}h^2f''(\eta),\quad \eta\in [a,b].$$

• 复化辛普森公式

  $$S_n = \frac{h}{6}\left[f(a)+4\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}}) + 2\sum_{k=1}^{n-1}f(x_k)+f(b)\right].$$

  其求积余项/误差为

  $$R_S = -\frac{b-a}{2880}h^4f^{(4)}(\eta),\quad \eta\in [a,b].$$

• 记还是好记的，记住梯形是1阶的，所以余项是2阶，辛普森是3阶所以余项是4阶。

4.5. 龙贝格求积公式

• 不在复习范围。

5. 线性方程组的数值解

5.1. 消元法

• 首先需要把原方程组换成矩阵形式，这样也就是求解$Ax = b$。

1. 顺序高斯消元

   就是线代中的非齐次方程解法，增广矩阵转为三角矩阵然后一一求解，求解前提是$A$的任意主子式$D_i\not = 0$。

   这里引入记符$a^{(i+1)}_{jk}$代表第$i$次迭代后的元素，$A^{(i+1)}$代表对原矩阵$A^{(1)}$的第$i$次消元/迭代步骤结果。

2. 列主元高斯消元

   直接消元运算过程可能会扩大误差，先找到列主要元素再消元，列主元为每列绝对值最大元素，使用这一行对其他行进行消元。

   这里注意$\det A\not = 0$。

5.2. LU分解法

• 每一步消元可以看成是左乘一个初等下三角矩阵$L_k$，

  $$A^{(i+1)} = L_{i}A^{(i)},\quad b^{(i)} = L_{i}b^{(i)}$$

  其中

  $$L_{i} = \begin{pmatrix} 1&&&&\\ 0&\cdots&&&\\ 0&\cdots&1&&\\ \vdots&\cdots&-l_{i+1,i}&\ddots&\\ \vdots&\cdots&\vdots&\vdots&\ddots\\ 0&\cdots&-l_{n,i}&\cdots&&1\\ \end{pmatrix},\quad l_{j,i} = a^{(i)}_{ji} / a^{(i)}_{ii},\quad (j=i+1,i+2,\dots,n)$$

  也就是第$i$次迭代时的初等矩阵$L_k$第$i$列为${1,l_{i+1,i},\dots}$。我们有$A^{(n)} = L_{n-1}L_{n-2}\cdots L_1 A^{(1)}$，则

  $$A^{(1)} = L_1^{-1}L_2^{-1}\cdot L_{n-1}^{-1}A^{(n)} = LA^{(n)} = LU$$

  令$UX = Y$，此时原方程$AX = b$可以写成

  $$\begin{cases} LY = b\\ UX = Y \end{cases}$$

• 实际解题时使用Doolittle或Courant对$A$进行分解得到$LU$。

1. Doolittle法

   对于

   

   有

   $$\begin{cases} u_{1j} &= a_{1j}\\ l_{i1} &= a_{i1}/u_{11} \end{cases}$$

   即$U$的第一行就是$A$第一行，$L$第一列就是$A$第一列分别除以$U$第一个元素。随后同样迭代有

   $$\begin{cases} u_{ij} &= a_{ij} - \sum_{k=1}^{i-1}l_{ik}u_{kj}\\ l_{ij} &= a_{ij} - \sum_{k=1}^{j-1}(l_{ik}u_{kj})/u_{jj} \end{cases}$$

   这里是$U$的第$i$行等于$A$第$i$行的元素减去$L$第$i$行和$U$第$j$列的内积。$L$的第$j$列是$A$第$i$行减去$L$第$i$行和$U$第$j$列的内积除以$U_{jj}$。

   • 但是上述计算太抽象了（实际上从代数理解是对$L$正交化的过程，但是手写计算太麻烦），一般我们使用类似增广矩阵变换的方式通过$[E, A]$得到$[L, U]$，例如

     

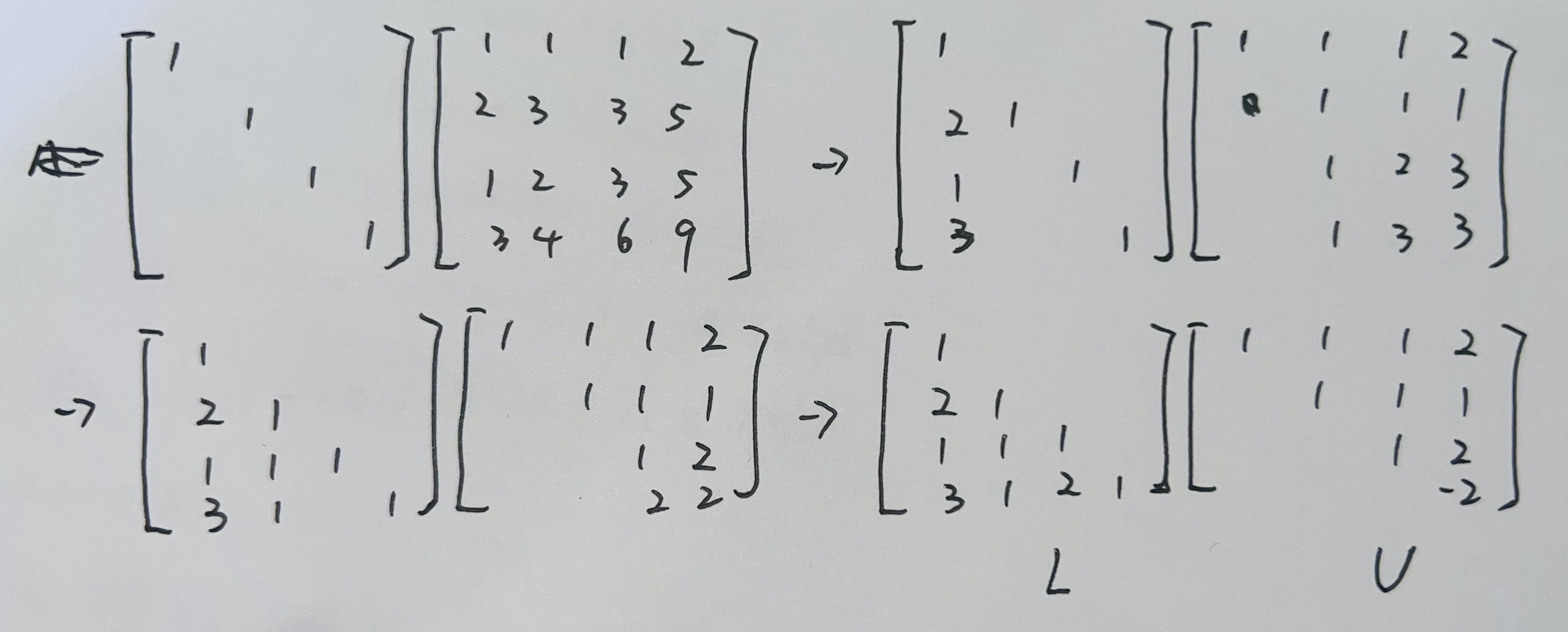
     其中每次计算右侧矩阵消元的倍数$k_j$更新到左边矩阵，同时更新右边矩阵为消元后结果，最终得到$L$和$U$。

2. Courant法

   和Doolittle类似，只是$U$变成了单位上三角，$L$变成了一般下三角。要算的话可以还是先Doolittle分解，然后对$U$每一列主元单位化，同时对$L$每一行乘上相应数值即可。

   例如上述就是$U$最后一列分别除以$-2$，$L$最后一行分别乘上$-2$即可。

3. Cholesky分解、追赶法

   不在复习范围。

5.3. 矩阵范数

• 定义向量p-范数为$\lVert x\rVert_2 = (\sum_{i=1}^n \lvert x_i\rvert^p)^{1/p}$，$p$取无穷时范数为$x$的最大元素绝对值。

  对于方阵有F-范数（Frobenius）

  $$\lVert A\rVert_F = \sqrt{\sum_{i=1}^n\sum_{j=1}^n{\lvert a_{ij}\rvert^2}}$$

  方阵其他范数有

  $$\begin{aligned} \lVert A\rVert_1 &= \max_{1\le j \le n}\sum_{i=1}^n\lvert a_{ij}\rvert \\ \lVert A\rVert_{\infty} &= \max_{1\le i \le n}\sum_{j=1}^n\lvert a_{ij}\rvert \\ \lVert A\rVert_{2} &= \sqrt{\max\lambda_i},\quad AA^T v = \lambda v \end{aligned}$$

  1-范数就是最大的列和（所以也叫列范数），$\infty$就是最大行和（所以也叫行范数），真正的2-范数为$AA^T$的最大特征值（求解方法是$\lvert \lambda I - AA^T\rvert = 0$）。

  推广到任意矩阵列范数和行范数任然成立。

5.4. 误差分析

• 不在复习范围内。

6. 线性方程组的迭代解

6.1. 基本迭代方法

• 对于$Ax = b$，设$x = Bx + f$，构造迭代

  $$x^{(k+1)} = Bx^{(k)} + f$$

1. Jacobi迭代

   方程组转化为

   $$\begin{cases} x_1^{(k+1)} &= \frac{1}{a_{11}}(-a_{12}x_2^{(k)} - \cdots - a_{1n}x_n^{(k)} + b_1)\\ x_2^{(k+1)} &= \frac{1}{a_{22}}(-a_{21}x_1^{(k)} - \cdots - a_{2n}x_n^{(k)} + b_2)\\ &\vdots\\ x_n^{(k+1)} &= \frac{1}{a_{nn}}(-a_{n1}x_1^{(k)} - \cdots - a_{n,n-1}x_{n-1}^{(k)} + b_n) \end{cases}$$

   解题时一般就是画迭代表，第一列为迭代次数$k$，每一行为$x$第$i$次迭代的解。

2. Gauss-Seidel法

   在迭代中使用最新解，例如计算出$x_1^{(k+1)}$后，对于$x_2^{(k+1)}$的计算中$x_1^{(k)}$使用$x_1^{(k+1)}$替代，后续同理。

6.2. 收敛判别

• 在Jacobi法中，将$A$记为$A = D - L - U$（这里的$L, U$分别是$A$的负值下上三角阵，和前面的LU分解法无关），$D$为对角阵。

  则$x^{(k+1)} = D^{-1}(L+U)x^{(k)} + D^{-1}b$，即$B = D^{-1}(L+U), f = D^{-1}b$。

• 对于Gauss-Seidel法，$B = (D-L)^{-1}U, f=(D-L)^{-1}b$

• 定义$\varepsilon^{(k+1)} = x^{(k+1)} - x^{*} = B\varepsilon^{(k)}$

  则有$\varepsilon^{(k)} = B^k\varepsilon^{(0)}$，迭代收敛的充要条件为

  $$\lim_{k\rightarrow \infty}\varepsilon^{(k)} = \lim_{k\rightarrow \infty}B^k\varepsilon^{(0)} = 0$$

  即$\rho(B)<1$，其中谱半径$\rho(B)$代表$B$的最大特征值绝对值。

• 解题的时候就是先分解$A$得到$B$矩阵，然后根据$\lvert \lambda I - B\lvert = 0$计算特征值，有些时候算不出来则通过罗尔定理判断根的区间，从而得到$\rho(B)$的不等关系进行判别（一般不用）。

• 还有如果$A$是严格对角占优，即对角元素绝对值均大于其他值，则收敛。

  或任意范数（解题一般计算1和无穷）$\lVert B\rVert < 1$，则收敛（但这个只是充分条件，不能判别发散）。

• 还有不可约对角占优、对称正定情况...应该用不上。

6.3. 松弛迭代法

• 不在复习范围内。

7. 非线性方程组求根

• 对于$f(x) = 0$，解为$x^{*}$，则$f(x)$可以写为

  $$f(x) = (x-x^{*})^m g(x),\quad g(x^{*})\not = 0$$

  若$m>1$则$x^{*}$为$m$重根。

7.1. 二分法

• 确定有根区间$[a,b]$，罗尔定理判定。

  假设$f(a)<0,f(b)>0$

  计算$c=(a+b)/2$，若$f(c)>0$，则$b=c$，反之$a=c$。

• 终止条件为$(b-a)/2^{n+1} \le \varepsilon$，得到迭代次数$\lceil n\rceil$。

7.2. 迭代法

• 将$f(x) = 0$改为$x = \varphi(x)$。即可进行迭代求解

  $$x_k = \varphi(x_{k-1})$$

  收敛的值$x^{*} = \varphi(x^{*})$为不动点。

• 收敛性

  若$\varphi(x)$在$[a,b]$上不动点存在且唯一，若

  1. $a\le \varphi(x)\le b$
  2. $\lvert \varphi '(x)\rvert \le L < 1$

  则该迭代式将收敛到不动点。反之则发散。

• 收敛速度

  若

  $$\lim_{k\rightarrow \infty}\frac{\vert x^{*}-x_{k+1}\vert}{\vert x^{*}-x_k\vert^p} = C$$

  则$\{x_k\}$收敛速度为$p$阶。

  这里计算时利用拉氏中值定理有

  $\vert x_{n+1} - x^{*}\vert = \vert \varphi(x_n) - \varphi(x^{*})\vert = \vert \varphi '(\xi_n)\vert \vert x_n-x^{*}\vert$。

  按此我们可以继续推广至$\varphi$的$p$阶导，原极限$=\vert \varphi^{(p)}(\xi_n)\vert = \vert \varphi^{(p)}(x^{*}) \vert \not = 0$。则若

  $$\varphi '(x^{*}) = \varphi ''(x^{*}) = \cdots = \varphi^{(p-1)}(x^{*}) = 0, \varphi^{p}(x^{*}) \not = 0$$

  有$x_{n+1}=\varphi(x_n)$为$p$阶收敛。

7.3. 迭代加速

• 计算了$x_k$和$x_{k+1}$后，由艾特金加速法计算

  $$\bar{x}_{k+1} = x_{k} - \frac{(x_{k+1} - x_k)^2}{x_{k+2} - 2x_{k+1} + x_k}$$

  将$\bar{x}_{k+1}$作为新的$x_{k+1}$再次计算$x_{k+2},x_{k+3}$更新得到$\bar{x}_{k+2}$。

7.4. 牛顿法

• 对于近似解$x_0$处一阶泰勒展开式有$f(x) + f'(x_0)(x-x_0) = 0$，则可得迭代公式

  $$x_{k+1} = x_k - \frac{f(x_k)}{f'(x_k)}$$

  牛顿法至少为二阶收敛。

8. 常微分方程

• 对于常微分方程$y' = f(x, y)$，我们将区间分为$n$份，步长为$h$，即$x_i = a+ih$。

8.1. 欧拉公式

• 将区间分为多个段求其斜率作为导数来迭代拟合。

  令$y_{i+1} = y_i + hf(x_i, y_i)$。迭代即可得到$\{x_i,y_i\}$对。

8.2. 梯形公式

• 将原微分方程两边积分，用梯形公式计算其积分项，有

  $$y_{i+1} = y_i + \frac{h}{2}[f(x_i, y_i)+f(x_{i+1},y_{i+1})]$$

8.3. 改进欧拉公式

• 上述梯形公式是个隐方程，所以我们用改进欧拉，计算出第一次迭代$\bar{y}_{i+1}$后带入梯形公式做一次校正。

  预测时$\bar{y}_{i+1} = y_i + hf(x_i,y_i)$， 校正为$y_{i+1} = y_i + \frac{h}{2}[f(x_i,y_i)+f(x_{i+1},\bar{y}_{i+1})]$

8.4. 龙格-库塔公式

• 不在复习范围内。