SG-PML吸收边界条件（边界反射问题）

原创Xenny2024年4月26日约 3322 字大约 14 分钟

SG-PML吸收边界条件（边界反射问题）

本文将对博文波动方程的有限差分解（地震数据正演）中提到的边界反射问题进行研究。解决地震正演中的边界反射带来的干扰。
首先我们要知道波为什么会反射，当从一种介质进入另一种介质时，在介质边界由于阻抗的不连续性，导致一部分能量继续进入新的介质称为透射波，一部分能量返回原介质称为反射波。而我们将需要了解反射部分具体是多少，以及如何消除边界反射问题。

吸收边界条件

自然界中地震波传播到介质边界（中断层）时，界面的波阻抗出现差异导致波发生反射和透射，地球介质可以看作“无限大”的区域，但在模拟计算中受到计算量的限制，模拟的传播区域大小是由界限的，这个人为截取的区域便是人工边界。
在人工边界处，边界外的波速可以看为0，即边界反射系数绝对值为1，此时表现在数值模拟中便产生了全反射现象，对地震正演中的波场计算将产生影响。此时我们需要引入吸收边界的概念来吸收掉这些传播至边界的波。
吸收边界条件即人为的在模拟计算区域的边界处设置一定厚度的吸收层，让能量在吸收层呈指数曲线衰减，最终在吸收层边界处近似衰减到0而避免边界反射。
注意这里我们的衰减函数也是有讲究的，因为如果衰减不够连续的话吸收层也将看成断层产生反射，虽然这里使用指数曲线进行衰减，但是实际模拟时还是会产生一定量的反射波。

PML

PML边界条件将波场分裂为垂直和平行的PML边界两部分，通过再分裂向量满足的微分方程中添加阻尼项得到PML中的微分方程。同时renger证明了如果不进行离散化PML条件可以完全无反射地吸收所有入射波。当然我们的模拟实现是没办法做到这一点的。

一维声波方程

这里我们先以一维声波为例说明PML边界条件思想，一维声波在均匀介质中的波动方程为^[1]
$\frac{1}{v^2(x)}\frac{\partial p(x,t)}{\partial t^2} = \frac{\partial^2 p(x,t)}{\partial x^2}\tag{1}$
其中 $v$ 代表速度， $p$ 代表波信息（即位移），我们添加一个中间变量 $A(x,t)$ 将上述方程改写为两个一阶偏微分方程
$\begin{aligned} \frac{\partial p(x,t)}{\partial t} = v^2(x)\frac{\partial A(x, t)}{\partial x}\\ \frac{\partial A(x,t)}{\partial x} = \frac{\partial p(x,t)}{\partial x} \end{aligned}\tag{2}$
显然式2再对 $t$ 求偏导即得式1，此时我们可以得到一个PML控制方程组
$\begin{aligned} \frac{\partial p^{*}(x,t)}{\partial t} + d(x)p^{*}(x,t) = v^2(x)\frac{\partial A^{*}(x,t)}{\partial x}\\ \frac{\partial A^{*}(x,t)}{\partial t} + d(x)A^{*}(x,t) = \frac{\partial p^{*}(x,t)}{\partial x} \end{aligned}\tag{3}$
其中 $p^{*}$ 代表式3方程的解， $d(x)$ 代表衰减系数，我们后续步骤的目的便是研究这个PML控制方程的解 $p^{*}$ 和原解 $p$ 的关系。对式3做关于时间的傅里叶变换得
$\begin{aligned} \mathrm{i}\omega\hat{p}^{*}(x, \omega) + d(x)\hat{p}^{*}(x,\omega) = v^2(x)\frac{\partial \hat{A}^{*}(x,\omega)}{\partial x}\\ \mathrm{i}\omega\hat{A}^{*}(x,\omega) + d(x)\hat{A}^{*}(x,\omega) = \frac{\partial \hat{p}^{*}(x,\omega)}{\partial x} \end{aligned}\tag{4}$
其中 $\hat{p}^{*}(x,\omega),\ \hat{A}^{*}(x,\omega)$ 分别代表 $p^{*}(x,\omega),\ A^{*}(x,\omega)$ 的傅里叶变换。再将实数空间域转换到复数空间域后的坐标得
$\widetilde{x}(x) = x - \frac{\mathrm{i}}{\omega}\int_{0}^x{d(s)}\mathrm{d}s\tag{5}$
则有
$\begin{aligned} \frac{\widetilde{x}(x)}{\partial x} &= 1 - \frac{\mathrm{i}d(x)}{\omega}\\ \frac{\partial \hat{A}^{*}(x)}{\partial x} = \frac{\partial \hat{A}^{*}(x)}{\partial \widetilde{x}}\frac{\widetilde{x}(x)}{\partial x} &= (1 - \frac{\mathrm{i}d(x)}{\omega})\frac{\partial \hat{A}^{*}(\widetilde{x})}{\partial \widetilde{x}}\\ \frac{\partial \hat{p}^{*}(x)}{\partial x} = \frac{\partial \hat{p}^{*}(x)}{\partial \widetilde{x}}\frac{\widetilde{x}(x)}{\partial x} &= (1 - \frac{\mathrm{i}d(x)}{\omega})\frac{\partial \hat{p}^{*}(\widetilde{x})}{\partial \widetilde{x}} \end{aligned}\tag{6}$
将式6带入式4得
$\begin{aligned} \mathrm{i}\omega \hat{p}^{*}(\widetilde{x}, \omega) = v^2(\widetilde{x})\frac{\partial \hat{A}^{*}(\widetilde{x})}{\partial \widetilde{x}}\\ \mathrm{i}\omega \hat{A}^{*}(\widetilde{x}, \omega) = \frac{\partial \hat{p}^{*}(\widetilde{x})}{\partial \widetilde{x}} \end{aligned}\tag{7}$
再对此式子做傅里叶逆变换到时间域上得
$\begin{aligned} \frac{\partial p^{*}(\widetilde{x}, t)}{\partial t} = v^2(\widetilde{x})\frac{\partial A^{*}(\widetilde{x}, t)}{\partial \widetilde{x}}\\ \frac{\partial A^{*}(\widetilde{x}, t)}{\partial t} = \frac{\partial p^{*}(\widetilde{x}, t)}{\partial \widetilde{x}} \end{aligned}\tag{8}$
可以发现式8与式2形式完全相同，设式2的解为 $p(x,t)$ ，式8的解为 $p(\widetilde{x},t)$ ，则式3的解 $p^{*}$ 为
$p(x - \frac{\mathrm{i}}{\omega}\int_p^x{d(s)}\mathrm{d}s, t)$
这代表的含义为我们可以先求式2的解（有限差分或者其他方法），再对解做坐标变换便可以得到式3的解。同时对于式2在均匀介质中有如下特解
$u(x,t) = p_0 \exp[-\mathrm{i}(k_xx-\omega t)]\tag{9}$
则对应的式3中的解为
$u^{*}(x,t) = p_0 \exp[-\mathrm{i}(k_x\widetilde{x}-\omega t)]\tag{10}$
将式5带入得
$u^{*}(x,t) = p_0\exp[-\mathrm{i}(k_xx - \omega t)-\frac{k_x}{\omega}\int_0^x{d(s)}\mathrm{d}s]\tag{11}$
可得上述解得振幅比（阻尼系数）为
$\frac{\lVert p^{*}(x, t)\rVert}{\lVert p(x,t)\rVert} = \exp\left[-\frac{k_x}{\omega}\int_0^x{d(s)}\mathrm{d}s \right]\tag{12}$
这代表引入 $d(x)$ 后波信号将按传播距离指数衰减。

交错网格

在求解二维声波方程的PML控制方程前，我们先来说明一下交错网格^[2]的概念，在求解高维时，我们会将波场分裂为各个维度的分量，例如二维中的 $x$ 方向和 $z$ 方向，将二阶微分方程变成两个一阶速度-应力方程进行求解。
对于二维声波方程，设 $p^x,p^z$ 分别为 $x,z$ 方向的波场位移分量，则对 $x$ 和 $z$ 方向的中心差分方程为
$\begin{cases} p_{i,j}^x = \frac{1}{\Delta x}\sum_{n=1}^N C_n^{(N)}(p^x_{i+\frac{2n-1}{2}, j} - p^x_{i-\frac{2n-1}{2},j})\\ p_{i,j}^z = \frac{1}{\Delta z}\sum_{n=1}^N C_n^{(N)}(p^z_{i, j+\frac{2n-1}{2}} - p^z_{i,j-\frac{2n-1}{2}})\tag{13} \end{cases}$
其中 $C_n^{(N)}$ 为差分系数（通过泰勒展开推导）， $2N$ 为差分空间阶数。
由式3有
$(\frac{\partial}{\partial t}+d_x)A = \frac{\partial p}{\partial x}\tag{14}$
设右式经过空间差分后近似结果为 $\blacksquare_k$ ，其中 $k$ 代表第 $k\Delta t$ 时刻。
则在交错网格下的PML控制方程近似方案如下
$(\frac{\partial}{\partial t}+d_x)A_k = \frac{A_{k+1/2}-A_{k-1/2}}{\Delta t} + d_xA_{k-1/2}\tag{15}$
带入式14得
$A_{k+1/2} = (1-\Delta t\cdot d_x)A_{k-1/2} + \Delta t\cdot \blacksquare|_k\tag{16}$

二维声波方程

那对于二维也是同理，对于二维声波方程
$\frac{1}{v^2(x, z)} \frac{\partial^2 p(x, z, t)}{\partial t^2} = \frac{\partial^2 p(x,z,t)}{\partial x^2} + \frac{\partial^2 p(x,z,t)}{\partial z^2}\tag{17}$
将 $p$ 分解为两个方向得分量 $p = p_x + p_z$ ，转为一阶速度——应力方程为
$\begin{aligned} \frac{\partial p_x}{\partial t} &= -\rho v^2(x,z)\frac{\partial A_x}{\partial x}\\ \frac{\partial p_z}{\partial t} &= -\rho v^2(x,z)\frac{\partial A_z}{\partial z}\\ \frac{\partial A_x}{\partial t} &= -\frac{1}{\rho}\frac{\partial p}{\partial x}\\ \frac{\partial A_z}{\partial t} &= -\frac{1}{\rho}\frac{\partial p}{\partial z} \end{aligned}\tag{18}$
对应的PML控制方程为
$\begin{aligned} \frac{\partial p_x}{\partial t} + d_xp_x &= -\rho v^2\frac{\partial A_x}{\partial x}\\ \frac{\partial p_z}{\partial t} + d_zp_z &= -\rho v^2\frac{\partial A_z}{\partial z}\\ \frac{\partial A_x}{\partial t} + d_xA_x &= -\frac{1}{\rho}\frac{\partial p}{\partial x}\\ \frac{\partial A_z}{\partial t} + d_zA_z &= -\frac{1}{\rho}\frac{\partial p}{\partial z} \end{aligned}\tag{19}$
空间上按照式13，时间上按照式16进行差分近似，得到交错网格有限差分声波方程时间递推方程为
$\begin{cases} A_x\vert_{i+1/2, j}^k = (1-\Delta t\cdot d_x)A_x\vert_{i+1/2,j}^{k-1} - \frac{\Delta t}{\rho\Delta x}\sum_{n=1}^N{C_n^{(N)}[p\vert_{i+1/2+\frac{2n-1}{2},j}^{k-1/2}-p\vert_{i+1/2-\frac{2n-1}{2},j}^{k-1/2}]}\\ A_z\vert_{i+1/2, j}^k = (1-\Delta t\cdot d_z)A_z\vert_{i,j+1/2}^{k-1} - \frac{\Delta t}{\rho\Delta z}\sum_{n=1}^N{C_n^{(N)}[p\vert_{i,j+1/2+\frac{2n-1}{2}}^{k-1/2}-p\vert_{i,j+1/2-\frac{2n-1}{2}}^{k-1/2}]}\\ p_x\vert_{i, j}^{k+1/2} = (1-\Delta t\cdot d_x)p_x\vert_{i,j}^{k-1/2} - \frac{\rho v^2\Delta t}{\Delta z}\sum_{n=1}^N{C_n^{(N)}[A_z\vert_{i,j+\frac{2n-1}{2}}^{k}-A_z\vert_{i,j-\frac{2n-1}{2}}^{k}]}\\ p_z\vert_{i, j}^{k+1/2} = (1-\Delta t\cdot d_z)p_z\vert_{i,j}^{k-1/2} - \frac{\rho v^2\Delta t}{\Delta z}\sum_{n=1}^N{C_n^{(N)}[A_z\vert_{i,j+\frac{2n-1}{2}}^{k}-A_z\vert_{i,j-\frac{2n-1}{2}}^{k}]}\tag{20} \end{cases}$

衰减系数

在PML中衰减系数 $d$ 满足 $d>0$ ，且在模拟时我们可以将PML区域分为三种不同情况
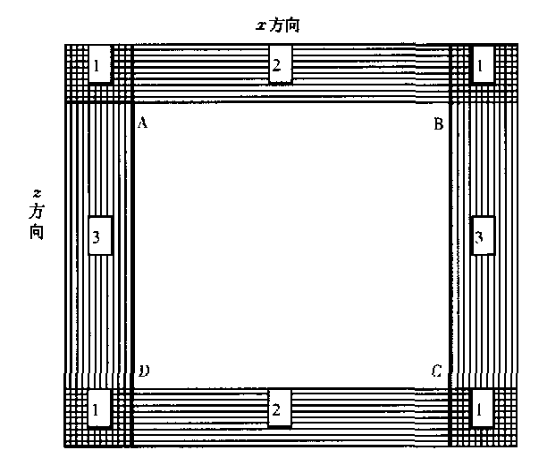
图1. PML吸收边界
对于图1中区域2满足 $d_x(x)=0,d_z(z)\not=0$ ，即垂直衰减水平方向不衰减，对于区域3则满足 $d_x(x)\not=0,d_z(z)=0$ 。而对于区域1则满足 $d_x(x)\not =0,d_z(z)\not= 0$ 。
一般选择^[3]
$d(x) = d_0\left(\frac{x}{\delta}\right)^n\tag{22}$
其中 $\sigma$ 为PML的厚度， $d_0$ 是理论反射系数 $R$ 中入射角 $\theta = 0$ 的情况，有
$R(\theta) = e^{-(2/(n+1))(d_0\delta/\epsilon_0 V_p)\cos{\theta}}\tag{23}$
其中 $V_p$ 为波速， $\epsilon_0$ 是啥我也不太清楚。当 $n$ 取 $n=2$ 时则有
$d_0 = -\log(R)\frac{3V_p}{2\delta}\tag{24}$

正演实验

先通过波场快照的动画，看看吸收效果。这里依然使用的是FCNVMB中的速度模型

结果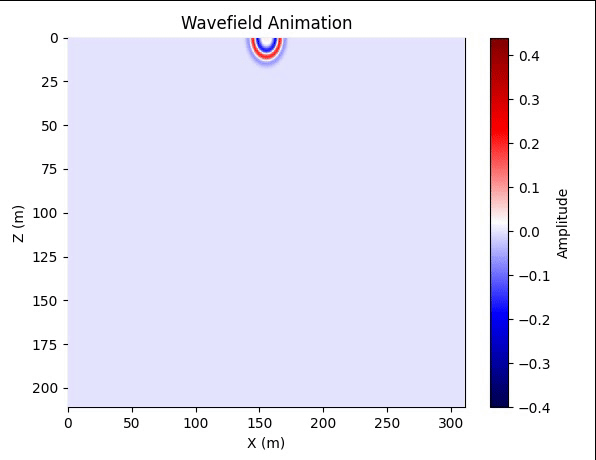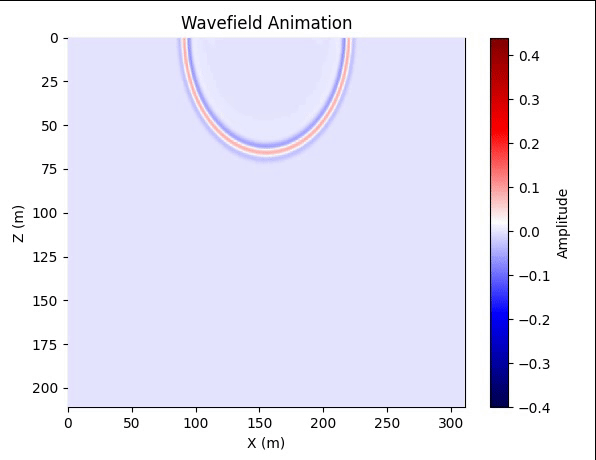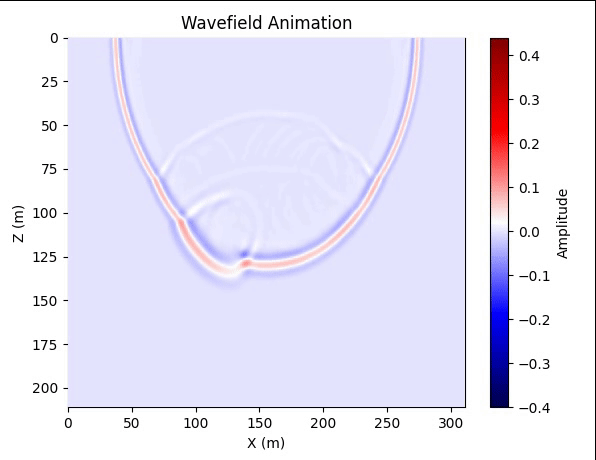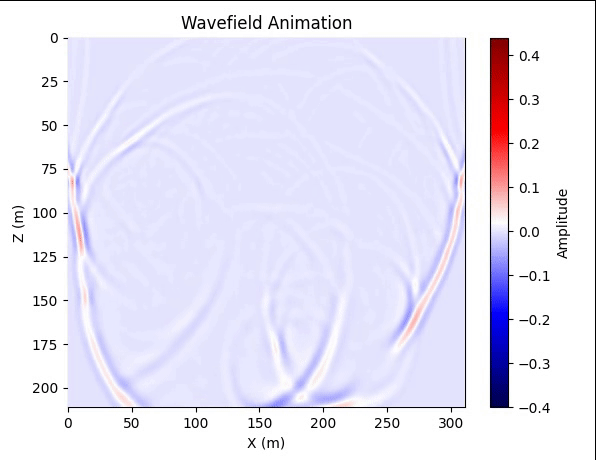

代码

from tqdm import tqdm
import numpy as np
import matplotlib.pylab as plt
import matplotlib.animation as animation
import scipy.io

data = scipy.io.loadmat(r'vmodel20.mat')

vmodel = data['vmodel']

h = 5                               # PML宽度
nodr = 3                            # 空间差分阶数/2
nz, nx = vmodel.shape
wave_source_ampl = 1
Nz, Nx = nz + 2 * h, nx + 2 * h

dx = dz = 10
dt = 0.001
nt = 1000

# 差分系数
B = np.zeros([nodr, 1])
B[0][0] = 1
A = np.zeros([nodr, nodr])
for i in range(nodr):
    A[i, :] = np.power(np.arange(1, 2 * nodr, 2), 2 * i + 1)
C = np.dot(np.linalg.inv(A), B).reshape(-1)

# 密度
rho = 10 * np.ones([Nz, Nx])  # 这里用均匀密度模型
vmodel_pad = np.pad(vmodel, [h, h], 'edge')

# 震源
sx = nx//2
sz = 0
f0 = 25.
t = dt * np.arange(1, nt + 1, 1)
t0 = 1 / f0
source_wav = (1 - 2 * np.power((np.pi * f0 * (t - t0)), 2)) * np.exp(-np.power((np.pi * f0 * (t - t0)), 2))


# 衰减系数
R = 0.001      # 理论反射系数

v_max = np.max(vmodel_pad)
dp_z = np.zeros([Nz, Nx])
dp_x = np.zeros([Nz, Nx])

dp0_z = -np.log(R)*3*v_max/(2*h*dz)
dp_z[:h, :] = np.dot(dp0_z * np.power(np.arange(h, 0, -1) / h, 2).reshape(-1, 1), np.ones([1, Nx]))
dp_z[(Nz - h):, :] = dp_z[h - 1::-1, :]

dp0_x = -np.log(R)*3*v_max/(2*h*dx)
dp_x[:, :h] = np.dot(np.ones([Nz, 1]), dp0_x * np.power(np.arange(h, 0, -1) / h, 2).reshape(1, -1))
dp_x[:, (Nx - h):] = dp_x[:, (h - 1)::-1]

# PML系数

rho1 = rho.copy()
rho2 = rho.copy()

Coeffi1 = (1 - dt * dp_x)
Coeffi2 = (1 - dt * dp_z)
Coeffi3 = 1 / rho1 / dx * dt
Coeffi4 = 1 / rho2 / dz * dt
Coeffi5 = rho * np.power(vmodel_pad, 2) / dx * dt
Coeffi6 = rho * np.power(vmodel_pad, 2) / dz * dt

NZ = Nz + 2 * nodr
NX = Nx + 2 * nodr
Znodes = np.arange(nodr, NZ - nodr, 1)
Xnodes = np.arange(nodr, NX - nodr, 1)
znodes = np.arange(nodr + h, nodr + h + nz)
xnodes = np.arange(nodr + h, nodr + h + nx)
sz_pad = nodr + h + sz
sx_pad = nodr + h + sx
Ut = np.zeros([NZ, NX])
Uz = np.zeros([NZ, NX])
Ux = np.zeros([NZ, NX])
Vz = np.zeros([NZ, NX])
Vx = np.zeros([NZ, NX])
U = -1 * np.ones([nz, nx, nt])
Psum = -1 * np.ones([Nz, Nx])

def index_2dim(matrix, height_index_array, width_index_array):
    return matrix[height_index_array[:, np.newaxis], width_index_array]

for cur_time in tqdm(range(nt)):
    Ux[sz_pad, sx_pad] = Ux[sz_pad, sx_pad] + wave_source_ampl * source_wav[cur_time] / 2
    Uz[sz_pad, sx_pad] = Uz[sz_pad, sx_pad] + wave_source_ampl * source_wav[cur_time] / 2
    Ut = Ux + Uz  # Ut is the combination of the two component matrices Ux and Uz
    U[:, :, cur_time] = index_2dim(Ut, znodes, xnodes)

    Psum[:, :] = 0
    for i in range(1, nodr + 1):
        Psum = Psum + C[i - 1] * (index_2dim(Ut, Znodes, Xnodes + i) - index_2dim(Ut, Znodes, Xnodes + 1 - i))
    Vx[nodr:NZ - nodr, nodr:NX - nodr] = Coeffi1 * index_2dim(Vx, Znodes, Xnodes) - Coeffi3 * Psum

    Psum[:, :] = 0
    for i in range(1, nodr + 1):
        Psum = Psum + C[i - 1] * (index_2dim(Ut, Znodes + i, Xnodes) - index_2dim(Ut, Znodes + 1 - i, Xnodes))
    Vz[nodr:NZ - nodr, nodr:NX - nodr] = Coeffi2 * index_2dim(Vz, Znodes, Xnodes) - Coeffi4 * Psum

    Psum[:, :] = 0
    for i in range(1, nodr + 1):
        Psum = Psum + C[i - 1] * (index_2dim(Vx, Znodes, Xnodes - 1 + i) - index_2dim(Vx, Znodes, Xnodes - i))
    Ux[nodr:NZ - nodr, nodr:NX - nodr] = Coeffi1 * index_2dim(Ux, Znodes, Xnodes) - Coeffi5 * Psum

    Psum[:, :] = 0
    for i in range(1, nodr + 1):
        Psum = Psum + C[i - 1] * (index_2dim(Vz, Znodes - 1 + i, Xnodes) - index_2dim(Vz, Znodes - i, Xnodes))
    Uz[nodr:NZ - nodr, nodr:NX - nodr] = Coeffi2 * index_2dim(Uz, Znodes, Xnodes) - Coeffi6 * Psum
            

fig, ax = plt.subplots()

im = ax.imshow(U[:, :, 0], extent=[0, Nx, Nz, 0], cmap='seismic', aspect='auto', vmin=-0.4, vmax=0.44)
ax.set_xlabel('X (m)')
ax.set_ylabel('Z (m)')
ax.set_title('Wavefield Animation')
fig.colorbar(im, ax=ax, label='Amplitude')

def init():
    im.set_data(U[:, :, 0])
    return im,
def update(frame):
    im.set_data(U[:, :, frame])
    return im,
ani = animation.FuncAnimation(fig, update, frames=range(1, nt),
                            init_func=init, blit=True, interval=20)
plt.show()

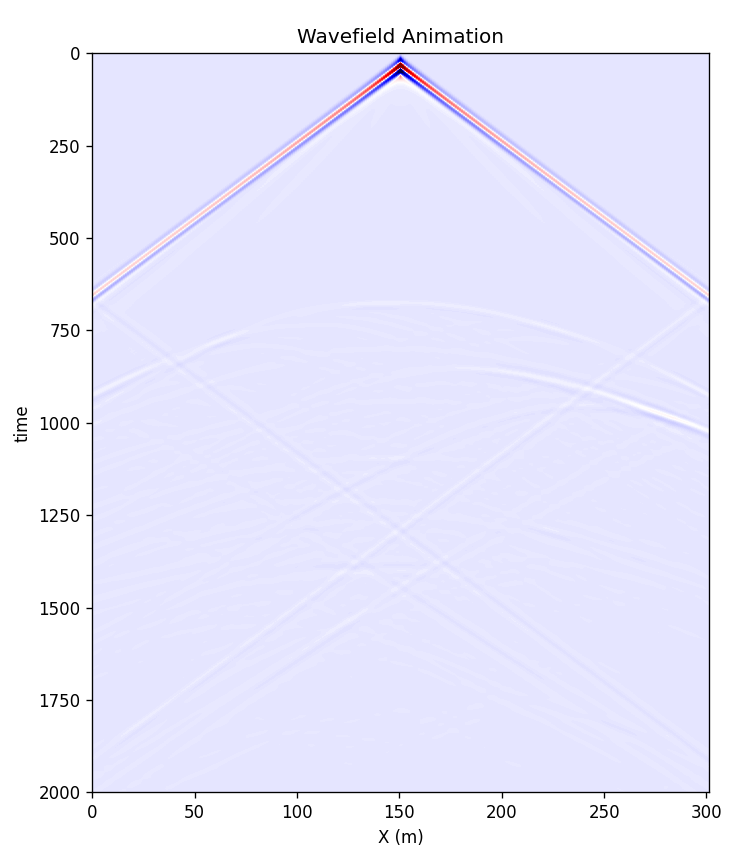
通过图2可以看出吸收效果还是非常好的，然后我们在地面设置检波器进行正演。

可以看到效果相比^[4]中没有吸收边界的情况好太多了。

参考

王守东. 声波方程完全匹配层吸收边界[J].石油地球物理勘探,2003(01):31-34+115-112. ↩︎
SG-PMLopen in new window ↩︎
Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of computational physics, 1994, 114(2): 185-200. ↩︎
波动方程的有限差分解（地震数据正演） ↩︎

SG-PML吸收边界条件（边界反射问题）

# SG-PML吸收边界条件（边界反射问题）

# 吸收边界条件

# PML

# 一维声波方程

# 交错网格

# 二维声波方程

# 衰减系数

# 正演实验

# 参考

SG-PML吸收边界条件（边界反射问题）

吸收边界条件

PML

一维声波方程

交错网格

二维声波方程

衰减系数

正演实验

参考