跳至主要內容

波动方程的有限差分解（地震数据正演）

原创Xenny约 3966 字大约 17 分钟FWI有限差分FWI

波动方程的有限差分解（地震数据正演）

有限差分法

  • 有限差分法是一种求解微分方程的数值方法，对于微分方程来说微分项很难处理，有限差分的思路便是用近似的方法处理微分项，例如对于一个一阶微分方程

    u′(x)+c(x)u(x)=f(x)u(a)=d(1) \begin{aligned} u^{'}(x) + c(x)u(x) &= f(x)\\ u(a) &= d \end{aligned}\tag{1}

    由导数定义有

    u′(x)=lim⁡Δx→0u(x+Δx)−u(x)Δx≈u(x+Δx)−u(x)Δx(2) u^{'}(x) = \lim\limits_{\Delta x \rightarrow 0}\frac{u(x+\Delta x) - u(x)}{\Delta x} \approx \frac{u(x + \Delta x) - u(x)}{\Delta x} \tag{2}

    这里的几何意义便是使用割线斜率近似替代切线斜率，显然Δx\Delta x越小则越精确，在后续求解中，我们将Δx\Delta x记为步长。

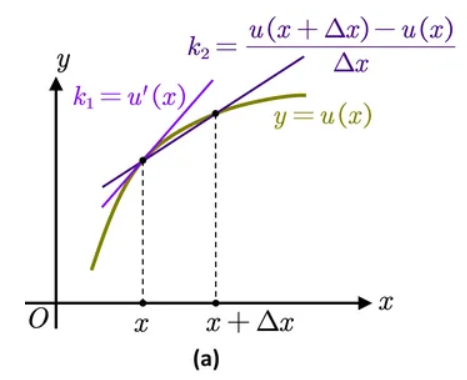
    图1. 微分近似表示
    图1. 微分近似表示

    由此在求解时我们要对求解区域进行离散化，即将区间按步长分为一个个离散点。设对于区间[a,b][a,b]共分为nn个区间，步长为hh，坐标为(x0,u0),(x1,u1),…,(xn,un){(x_0, u_0), (x_1, u_1),\dots, (x_n,u_n)}，则我们可以得到各点处导数值得近似表示

    ui′=1h(ui+1−ui)(3) u_i^{'} = \frac{1}{h}(u_{i+1}- u_i)\tag{3}

    带入原方程得

    (ui+1−ui)/h+c(xi)ui=f(xi) (u_{i+1} - u_i)/h + c(x_i)u_i = f(x_i)

    其中xi=a+ih,i=0,1,2,…x_i = a+ih, i=0,1,2,\dots，则我们有nn个方程(i=0,1,…,n−1)(i=0,1,\dots,n-1)，包含nn个未知数(u1,u2,…,un)(u_1,u_2,\dots,u_n)。此时我们对方程变形得到

    ui+1=(1−hc(xi))ui+hf(xi)(4) u_{i+1} = (1-hc(x_i))u_i + hf(x_i)\tag{4}

    则上述方程组可写为矩阵的形式

    [1C11⋱⋱cn−11](u1u2⋮nn)=(hf(x0)hf(x1)⋮hf(xn−1))−(C0u00⋮0)(5) \begin{bmatrix} 1&&&\\ C_1&1&&\\ &\ddots&\ddots&\\ &&c_{n-1}&1 \end{bmatrix}\begin{pmatrix} u_1\\ u_2\\ \vdots\\ n_n \end{pmatrix} = \begin{pmatrix} hf(x_0)\\ hf(x_1)\\ \vdots\\ hf(x_{n-1}) \end{pmatrix} - \begin{pmatrix} C_0u_0\\ 0\\ \vdots\\ 0 \end{pmatrix}\tag{5}

    其中Ci=hc(xi)−1C_i = hc(x_i)-1，上述矩阵方程记为Au=F\mathbf{A}\boldsymbol{u} = \mathbf{F}，则解为u=A−1F\boldsymbol{u} = \mathbf{A}^{-1}\mathbf{F}（这里显然r(A)=nr(\mathbf{A}) = n即可逆）。

差分公式

  • 对于有限差分来说，其原理大致和上述相同，只是不是简单的使用割线斜率来表示切线斜率，而是使用泰勒级数对函数进行展开，从而得到各阶的近似公式也即“差分公式”。

    由泰勒级数我们有函数u(x)u(x)在点xx处的展开为（前提是该点邻域nn阶可导）

    u(x+h)=u(x)+hu′(x)+h22u′′(x)+⋯+hkk!u(n)(x)+Rn(6) u(x+h) = u(x) + hu^{'}(x) + \frac{h^2}{2}u^{''}(x) + \cdots + \frac{h^k}{k!}u^{(n)}(x) + R_n\tag{6}

    根据需要来截取不同的近似阶数。

  • 对于一阶微分，则有

    u(x+h)=u(x)+hu′(x)+h22u′′(x+ξ)(7) u(x+h) = u(x) + hu^{'}(x) + \frac{h^2}{2}u^{''}(x+\xi)\tag{7}

    其中ξ∈(0,h)\xi \in (0,h)，则变形即可得到一阶微分的向前差分公式：

    uF′(x)=u(x+h)−u(x)h−h2u′′(x+ξ)(8) u^{'}_F(x) = \frac{u(x+h)-u(x)}{h} - \frac{h}{2}u^{''}(x+\xi)\tag{8}

    同时将hh替换为−h-h，我们可以得到一阶微分的向后差分公式：

    uB′(x)=u(x)−u(x−h)h+h2u′′(x+ξ)(9) u^{'}_B(x) = \frac{u(x) - u(x-h)}{h} + \frac{h}{2}u^{''}(x+\xi)\tag{9}

    联立式(8)与式(9)，可以得到一阶微分的中心差分公式：

    uC′(x)=u(x+h)−u(x−h)2h+O(h2)(10) u^{'}_C(x) = \frac{u(x+h) - u(x-h)}{2h} + O(h^2)\tag{10}

    同理也可以得到其他高阶微分的差分公式，其实和高数里面利用泰勒求高阶导类似。

偏微分方程

  • 不过在后面的波动方程中，它是一个偏微分方程，所以我们还需要了解偏微分方程中的有限差分是如何近似的。

    偏微分的概念其实也就是提高了维度，在一维中我们是得到导数近似的差分公式后对原方程离散化处理求解，这里也是一样的，假设我们要求一个二元偏微分方程，此时则将求解区域x∈[a,b],y∈[c,d]x\in [a,b], y\in [c,d]进行网格化，在每个格点使用微分差分公式来近似表达偏导进行求解。

    例如对于方程组

    {Δu=f(x,y)u(0,y)=c(y), u(a,y)=d(y)u(x,0)=g(x), u(x,b)=h(x)(11) \begin{cases} \Delta u = f(x, y)\\ u(0,y) = c(y),\ u(a,y) = d(y)\\ u(x,0) = g(x),\ u(x,b) = h(x) \end{cases}\tag{11}

    其中x∈[0,a],y∈[0,b]x \in [0,a], y \in[0,b]，则分别将x,yx,y分为m,nm,n份，记为xi(i=0,1,…,m),yj(j=0,1,…,n)x_i(i=0,1,\dots,m), y_j(j=0,1,\dots,n)。

  • 由二阶微分中心差分公式有

    ∂2u∂x2=ui+1,j−2ui,j+ui−1,jhx2,∂2u∂y2=ui,j+1−2ui,j+ui,j−1hy2(12) \frac{\partial^2 u}{\partial x^2} = \frac{u_{i+1,j} - 2u_{i,j} + u_{i-1,j}}{h_{x}^2}, \frac{\partial^2 u}{\partial y^2} = \frac{u_{i,j+1} - 2u_{i,j} + u_{i,j-1}}{h_{y}^2}\tag{12}

    其中hx=a/m,hy=b/nh_x=a/m,h_y=b/n分别为xx方向和yy方向的步长。令p=1/hx2,q=1/hy2,r=−2(p+1),f(xi,yj)=fi,jp=1/h_x^2,q=1/h_y^2,r=-2(p+1),f(x_i,y_j) = f_{i,j}和式(12)带入式(11)得

    {qui,j−1+pui−1,j+rui,j+pui+1,j+qui,j+1=fi,ju0,j=cj, um,j=djui,0=gi, ui,n=hi(13) \begin{cases} qu_{i,j-1} + pu_{i-1,j} + ru_{i,j} + pu_{i+1,j} + qu_{i,j+1} = f_{i,j}\\ u_{0,j} = c_j,\ u_{m,j} = d_j\\ u_{i,0} = g_i,\ u_{i,n} = h_i \end{cases}\tag{13}

    显然我们可以得到m×nm\times n个这样的方程组，我们将上述方程组转换为矩阵形式为

    [UVVUV⋱⋱⋱VUVVU](u⃗i,1u⃗i,2⋮u⃗i,n−2u⃗i,n−1)=(f⃗i,1f⃗i,2⋮f⃗i,n−2f⃗i,n−1)−q(u⃗i,00⋮00)−q(00⋮0u⃗i,m) −p(u⃗0,1u⃗0,2⋮u⃗0,n−2u⃗0,n−1)−p(u⃗m,1u⃗m,2⋮u⃗m,n−2u⃗m,n−1)(14) \begin{bmatrix} \mathbf{U}&\mathbf{V}&\\ \mathbf{V}&\mathbf{U}&\mathbf{V}&\\ &\ddots&\ddots&\ddots\\ &&\mathbf{V}&\mathbf{U}&\mathbf{V}\\ &&&\mathbf{V}&\mathbf{U} \end{bmatrix}\begin{pmatrix} \vec{u}_{i,1}\\ \vec{u}_{i,2}\\ \vdots\\ \vec{u}_{i,n-2}\\ \vec{u}_{i,n-1} \end{pmatrix} = \begin{pmatrix} \vec{f}_{i,1}\\ \vec{f}_{i,2}\\ \vdots\\ \vec{f}_{i,n-2}\\ \vec{f}_{i,n-1}\\ \end{pmatrix} - q\begin{pmatrix} \vec{u}_{i,0}\\ 0\\ \vdots\\ 0\\ 0 \end{pmatrix} - q\begin{pmatrix} 0\\0\\\vdots\\0\\\vec{u}_{i,m} \end{pmatrix}\\\ \\- p\begin{pmatrix} \vec{u}_{0,1}\\ \vec{u}_{0,2}\\ \vdots\\ \vec{u}_{0,n-2}\\ \vec{u}_{0,n-1} \end{pmatrix}- p\begin{pmatrix} \vec{u}_{m,1}\\ \vec{u}_{m,2}\\ \vdots\\ \vec{u}_{m,n-2}\\ \vec{u}_{m,n-1} \end{pmatrix}\tag{14}

    其中

    U=[rpprp⋱⋱⋱prppr](m−1)×(m−1),V=[qq⋱qq](m−1)×(m−1)u⃗i,j=(u1,j,u2,j,…,um−1,j)T,f⃗i,j=(f1,j,f2,j,…,fm−1,j)Tu⃗i,0=(u1,0,u2,0,…,um−1,0)T,u⃗i,n=(u1,n,u2,n,…,um−1,n)Tu⃗0,j=(u0,j,0,…,0)T,u⃗m,j=(0,0,…,0,um,j)T \mathbf{U} = \begin{bmatrix} r&p&\\ p&r&p\\ &\ddots&\ddots&\ddots&\\ &&p&r&p\\ &&&p&r \end{bmatrix}_{(m-1)\times (m-1)},\mathbf{V} = \begin{bmatrix} q\\ &q\\ &&\ddots\\ &&&q\\ &&&&q \end{bmatrix}_{(m-1)\times (m-1)}\\ \vec{u}_{i,j} = (u_{1,j}, u_{2,j}, \dots, u_{m-1,j})^T, \vec{f}_{i,j} = (f_{1,j},f_{2,j},\dots,f_{m-1,j})^T\\ \vec{u}_{i,0} = (u_{1,0}, u_{2,0}, \dots, u_{m-1,0})^T, \vec{u}_{i,n} = (u_{1,n},u_{2,n},\dots,u_{m-1,n})^T\\ \vec{u}_{0,j} = (u_{0,j}, 0,\dots, 0)^T,\vec{u}_{m,j} = (0,0,\dots,0,u_{m,j})^T

  • 这里用的是知乎文章[1]的例子，里面没给推导过程。这里记录一下推导过程

    首先是固定jj，将jj看成常量转为矩阵形式有

    [rpprp⋱⋱⋱prppr](u1,ju2,j⋮um−2,jum−1,j)=(f1,jf2,j⋮fm−2,jfm−1,j)−q(u1,j−1u2,j−1⋮um−2,j−1um−1,j−1)−q(u1,j+1u2,j+1⋮um−2,j+1um−1,j+1)−p(u0,j0⋮00)−p(00⋮0um,j)(15) \begin{bmatrix} r&p&\\ p&r&p\\ &\ddots&\ddots&\ddots&\\ &&p&r&p\\ &&&p&r \end{bmatrix}\begin{pmatrix} u_{1,j}\\ u_{2,j}\\ \vdots\\ u_{m-2,j}\\ u_{m-1,j} \end{pmatrix} = \begin{pmatrix} f_{1,j}\\ f_{2,j}\\ \vdots\\ f_{m-2,j}\\ f_{m-1,j} \end{pmatrix} - q\begin{pmatrix} u_{1,j-1}\\ u_{2,j-1}\\ \vdots\\ u_{m-2,j-1}\\ u_{m-1,j-1} \end{pmatrix} - q\begin{pmatrix} u_{1,j+1}\\ u_{2,j+1}\\ \vdots\\ u_{m-2,j+1}\\ u_{m-1,j+1} \end{pmatrix}\\ -p\begin{pmatrix} u_{0,j}\\ 0\\ \vdots\\ 0\\0 \end{pmatrix}-p\begin{pmatrix} 0\\ 0\\ \vdots\\ 0\\ u_{m,j} \end{pmatrix}\tag{15}

    这样的矩阵方程有n−1n-1个，此时便可以将每个向量换成上面的记法，

    Uu⃗i,j=f⃗i,j−Vu⃗i,j−1−Vu⃗i,j+1−pu⃗0,j−pu⃗m,j(16) \mathbf{U}\vec{u}_{i,j} = \vec{f}_{i,j} - \mathbf{V}\vec{u}_{i,j-1} - \mathbf{V}\vec{u}_{i,j+1} - p\vec{u}_{0,j} - p\vec{u}_{m,j}\tag{16}

    此时便可以固定ii，将ii看成常量再转为一个矩阵方程

    [UVVUV⋱⋱⋱VUVVU](u⃗i,1u⃗i,2⋮u⃗i,n−2u⃗i,n−1)=(f⃗i,1f⃗i,2⋮f⃗i,n−2f⃗i,n−1)−p(u⃗0,1f⃗0,2⋮f⃗0,n−2f⃗0,n−1)−p(u⃗m,1f⃗m,2⋮f⃗m,n−2f⃗m,n−1)−q(u⃗i,00⋮00)−q(00⋮0u⃗i,m)(17) \begin{bmatrix} \mathbf{U}&\mathbf{V}\\ &\mathbf{V}&\mathbf{U}&\mathbf{V}\\ &&\ddots&\ddots&\ddots\\ &&&\mathbf{V}&\mathbf{U}&\mathbf{V}\\ &&&&\mathbf{V}&\mathbf{U} \end{bmatrix}\begin{pmatrix} \vec{u}_{i,1}\\ \vec{u}_{i,2}\\ \vdots\\ \vec{u}_{i,n-2}\\ \vec{u}_{i,n-1} \end{pmatrix} = \begin{pmatrix} \vec{f}_{i,1}\\ \vec{f}_{i,2}\\ \vdots\\ \vec{f}_{i,n-2}\\ \vec{f}_{i,n-1}\\ \end{pmatrix} - p\begin{pmatrix} \vec{u}_{0,1}\\ \vec{f}_{0,2}\\ \vdots\\ \vec{f}_{0,n-2}\\ \vec{f}_{0,n-1}\\ \end{pmatrix} - p\begin{pmatrix} \vec{u}_{m,1}\\ \vec{f}_{m,2}\\ \vdots\\ \vec{f}_{m,n-2}\\ \vec{f}_{m,n-1}\\ \end{pmatrix}\\ - q\begin{pmatrix} \vec{u}_{i,0}\\ 0\\ \vdots\\ 0\\ 0 \end{pmatrix} - q\begin{pmatrix} 0\\0\\\vdots\\0\\\vec{u}_{i,m} \end{pmatrix}\tag{17}

    至此便得到了该二阶微分方程的解。

误差分析

  • 对于的二维泊松方程，取f(x,y)=−2π2sin⁡(πx)sin⁡(πy),c(y)=d(y)=g(x)=h(x)=0,(x,y)∈[0,1]×[0,1]f(x,y) = -2\pi^2\sin(\pi x)\sin(\pi y),c(y)=d(y)=g(x)=h(x)=0,(x,y)\in [0,1]\times [0,1]，此时有对应的解析解u(x,y)=sin⁡(πx)sin⁡(πy)u(x,y) = \sin(\pi x)\sin(\pi y)，令m=n=100m=n=100时解析解和FDM得到的解对比如图2所示。

    结果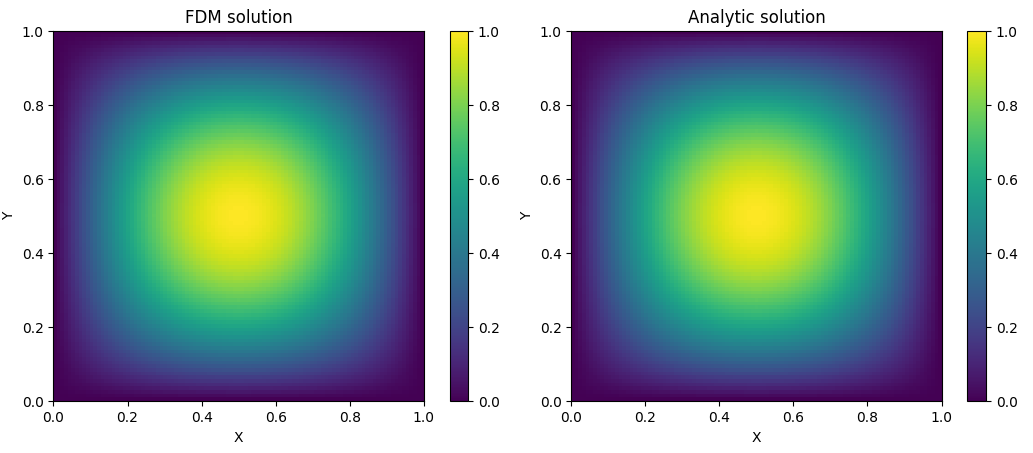
    图2. FDM和解析解结果对比
    图2. FDM和解析解结果对比

    可以看出几乎没有什么误差，同时还可以来分析一下不同m,nm,n取值时的误差，这里选择使用L2距离计算误差，取m=n=sm=n=s，得到的误差变化如图3所示。

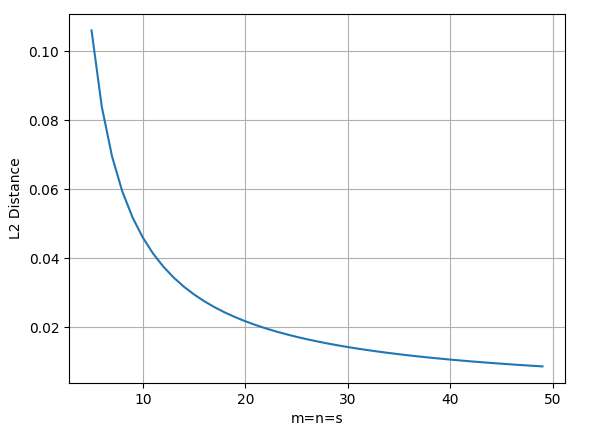
    图3. L2距离变化
    图3. L2距离变化

地震正演

雷克子波

  • 雷克（Ricker）子波是地震子波的一种，是由震源激发、经地下传播再被地面捕获的地震波。在FWI中，通常用地震子波于反射系数的卷积表示地震数据。

    其表达式为

    s(t)=e−(πft)2(1−2(πft)2) s(t) = e^{-(\pi f t)^2}(1-2(\pi f t)^2)

    图像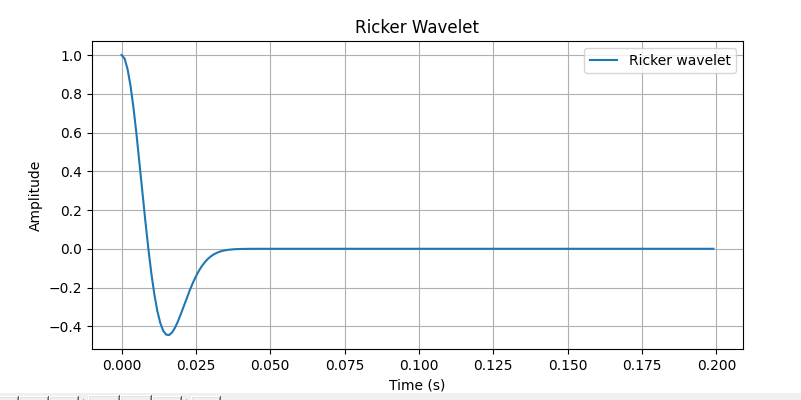
    图4. 雷克子波
    图4. 雷克子波

    这是雷克子波的一个周期，我们可以将输出范围调节至[-0.2, 0.2]来查看雷克子波的全貌。

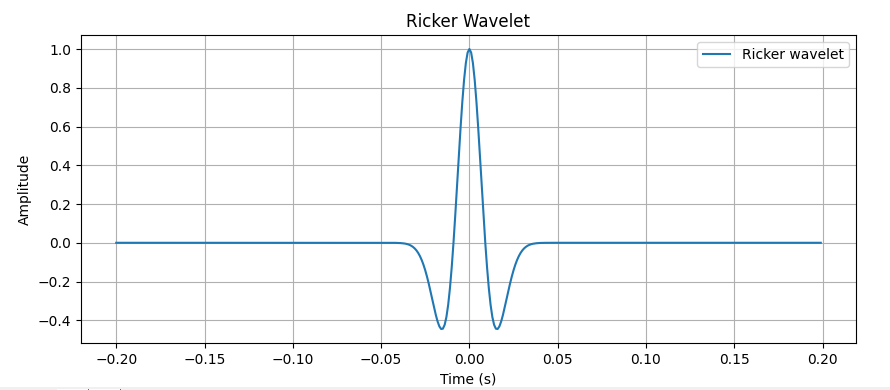
    图5. 雷克子波对称区间图像
    图5. 雷克子波对称区间图像

    在正演时我们将使用雷克子波作为初始震源，然后通过求解波动方程得到在指定的速度模型中波信号的变化。

波动方程

  • 首先先看一下声波波动方程：

    1v2(x,z)∂2p(x,z,t)∂t2=∂2p(x,z,t)∂x2+∂2p(x,z,t)∂z2(19) \frac{1}{v^2(x, z)} \frac{\partial^2 p(x, z, t)}{\partial t^2} = \frac{\partial^2 p(x,z,t)}{\partial x^2} + \frac{\partial^2 p(x,z,t)}{\partial z^2}\tag{19}

    其中(x,z)(x,z)代表空间坐标，pp代表波场，vv表示速度场，tt代表时间。而我们要做的便是求解该微分方程从速度vv反解得到pp。

  • 由二阶微分中心差分公式有

    ∂2p∂x2=p(x+1,z,t)−2p(x,z,t)+p(x−1,z,t)hx2∂2p∂z2=p(x,z+1,t)−2p(x,z,t)+p(x,z−1,t)hz2∂2p∂t2=p(x,z,t+1)−2p(x,z,t)+p(x,z,t−1)ht2(20) \begin{aligned} \frac{\partial^2 p}{\partial x^2} = \frac{p(x+1,z,t) - 2p(x,z,t) + p(x-1,z,t)}{h_x^2}\\ \frac{\partial^2 p}{\partial z^2} = \frac{p(x,z+1,t) - 2p(x,z,t) + p(x,z-1,t)}{h_z^2}\\ \frac{\partial^2 p}{\partial t^2} = \frac{p(x,z,t+1) - 2p(x,z,t) + p(x,z,t-1)}{h_t^2} \end{aligned}\tag{20}

    代入原方程得

    1v2(x,z)p(x,z,t+1)−2p(x,z,t)+p(x,z,t−1)ht2=p(x+1,z,t)−2p(x,z,t)+p(x−1,z,t)hx2+p(x,z+1,t)−2p(x,z,t)+p(x,z−1,t)hz2(20) \frac{1}{v^2(x, z)} \frac{p(x,z,t+1) - 2p(x,z,t) + p(x,z,t-1)}{h_t^2}\tag{20} = \\\frac{p(x+1,z,t) - 2p(x,z,t) + p(x-1,z,t)}{h_x^2} + \frac{p(x,z+1,t) - 2p(x,z,t) + p(x,z-1,t)}{h_z^2}

    整理可得

    p(x,z,t+1)=2p(x,z,t)−p(x,z,t−1)+v2(x,z)ht2hz2(p(x,z+1,t)−2p(x,z,t)+p(x,z−1,t))+v2(x,z)ht2hx2(p(x+1,z,t)−2p(x,z,t)+p(x−1,z,t)) \begin{aligned} p(x,z,t+1) &= 2p(x,z,t) - p(x,z,t-1)\\ &+\frac{v^2(x, z)h_t^2}{h_z^2}(p(x,z+1,t) - 2p(x,z,t) + p(x,z-1,t))\\ &+\frac{v^2(x, z)h_t^2}{h_x^2}(p(x+1,z,t) - 2p(x,z,t) + p(x-1,z,t)) \end{aligned}

    这样我们便得到了在地震正演中如何任意位置上一时刻到下一时刻的波信号变化。

单炮数据正演

  • 首先需要生成速度模型，这里我直接用了链接1[2]的模拟速度模型(vmodel20.mat)。

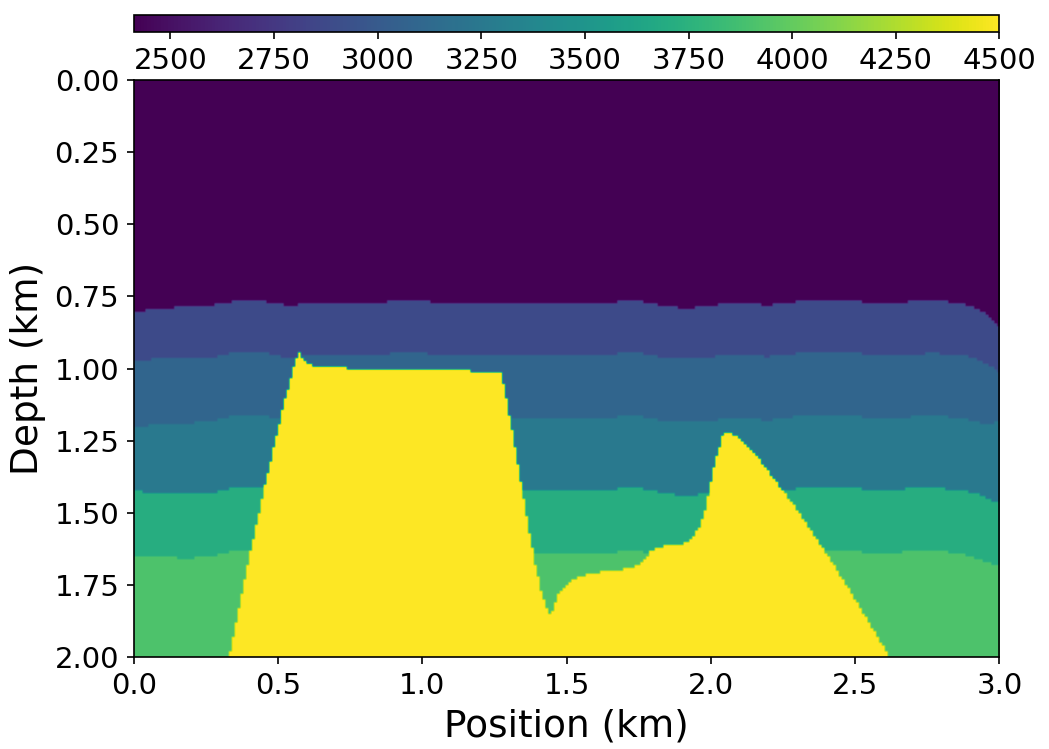
    图6. 速度模型
    图6. 速度模型

    然后我们编写python代码进行正演，然后我们可以得到如下结果

    结果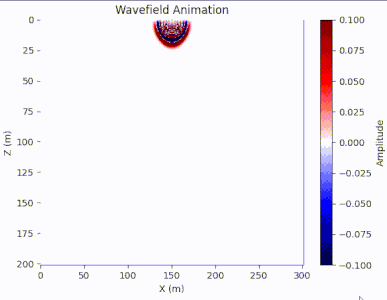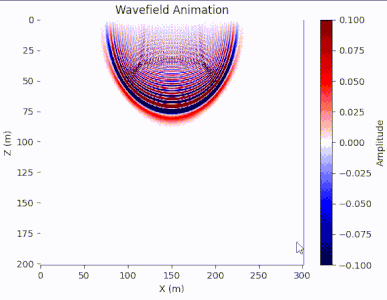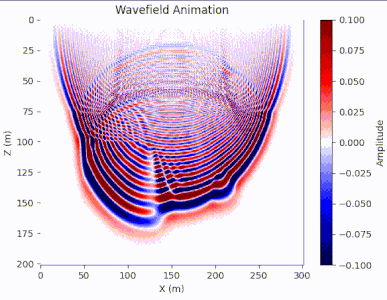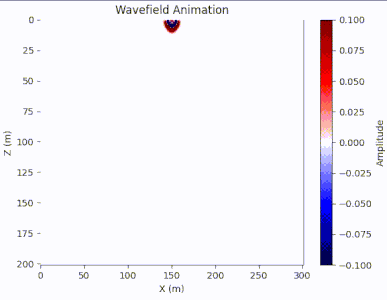
    图7. 波场快照动画
    图7. 波场快照动画

    波场快照即tt时刻波的传播情况，这里我们用叠加动画的方式进行展示。可以看到震源处的波随着时间而传播开，在通过不同的介质时也获得了不同的速度得到不同的波形以及形成反射波，但是会发现波在碰到边界后也产生反射波，这是因为正常的波在地下传播是无限的，但我们人为截取了一个边界导致边界反射问题，这个问题将在后续单独的篇章中记录。

  • 这里得到了波场快照之后，我们便可以设置检波点来模拟实际获取数据的效果，因为波场是我们使用波动方程推导的，而实际获取数据时需要在地面或地下设置具体的检波器来获取数据。检波器的设置很简单，获取固定位置的波场数据即可。

    结果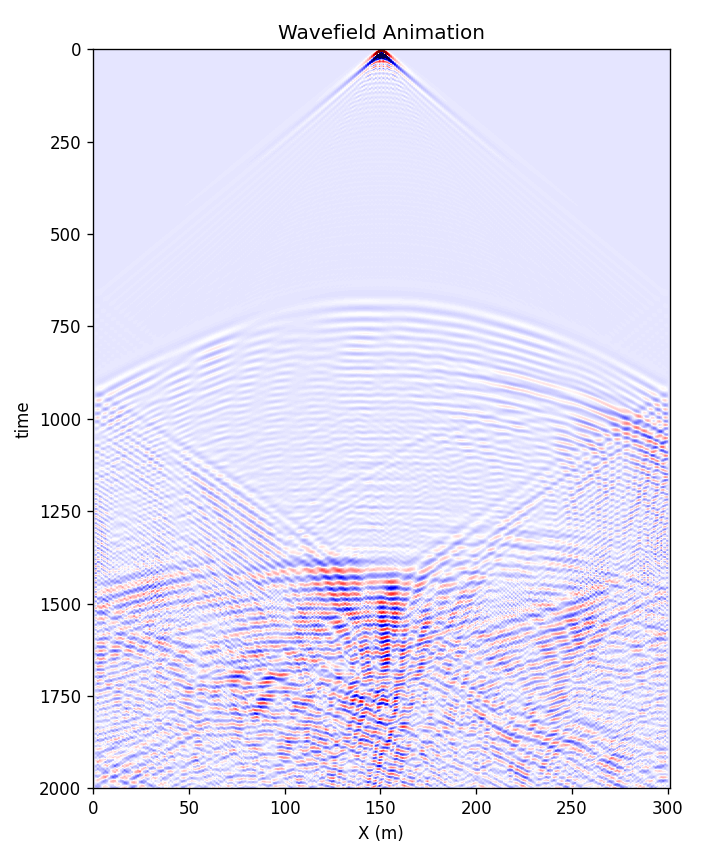
    图8. 单炮数据正演
    图8. 单炮数据正演

参考

  1. 微分方程数值求解——有限差分法open in new window ↩︎

  2. FCNVMB-Deep-learning-based-seismic-velocity-model-building open in new window ↩︎

Xenny
https://xenny.wiki/posts/fwi/experiment/fdm.html
本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Xenny 的博客！
2024 © Xenny All rights reserved. 著作权归 Xenny 所有