Overcoming catastrophic forgetting in neural networks

• arxiv: 1612.00796

• 序列化的学习方法对AI发展至关重要。而目前连接型的神经网络存在灾难性遗忘问题，本文提出一种方式可以克服这个问题，使得训练的网络能够长时间保存知识。该方法通过选择性地减缓任务的重要程度来记住旧任务。通过MNIST数据集的分类任务和Atari 2600游戏任务实验证明了该方法是可扩展和有效的。

EWC

核心思想

• 与人工神经网络形成鲜明对比的是，人类和其他动物似乎能够以持续的方式学习。最近的证据表明，哺乳动物的大脑可以通过保护新皮层回路中先前获得的知识来避免灾难性的遗忘。当小鼠获得一项新技能时，一定比例的兴奋性突触得到加强;这表现为神经元的单个树突棘体积的增加。至关重要的是，尽管随后学习了其他任务，但这些扩大的树突棘仍然存在，这是几个月后保持性能的原因。当这些刺被选择性地“擦除”时，相应的技能就会被遗忘。这提供了因果证据，表明支持保护这些增强突触的神经机制对于保持任务绩效至关重要。总之，这些实验发现与神经生物学模型一起表明，哺乳动物新皮层的持续学习依赖于任务特异性突触巩固的过程，其中关于如何执行先前获得的任务的知识被持久地编码在一定比例的突触中，这些突触的可塑性降低，因此在很长一段时间内都很稳定。该算法会根据某些权重对以前看到的任务的重要性来减慢学习速度。我们展示了如何在监督学习和强化学习问题中使用EWC，以按顺序训练多个任务，而不会忘记较旧的任务，这与以前的深度学习技术形成鲜明对比。\footnote

• 本文提出了一种弹性权重整合算法（EWC），核心思想是降低重要权重的学习率来减少遗忘。

  

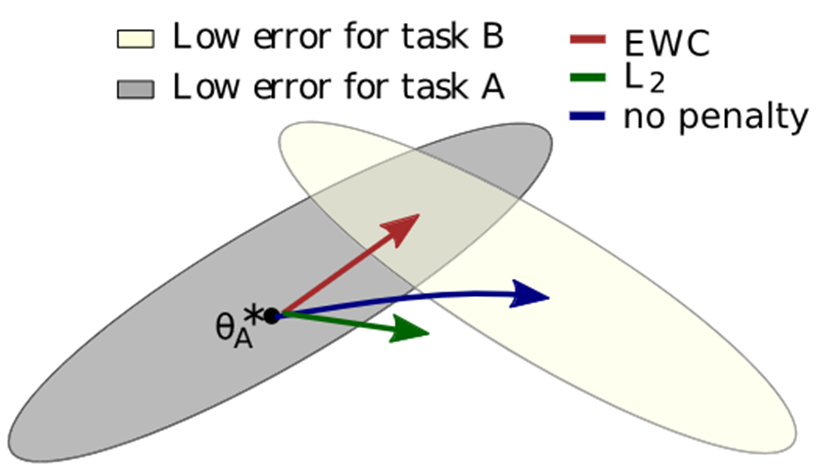
  alt text

  对于不同的两个任务我们假设其数据集分布如图1所示。其中灰色区域代表旧任务的低误差区域（即较优解域），黄色区域为新任务分布。如果直接使用旧任务的权重初始化网络，用新任务Fine-tune的话，优化方向如蓝色箭头所示，即网络只会认为黄色区域是优化目标而前进，会快速脱离灰色区域（灾难性遗忘）。 如果每个参数都用相同的系数约束的话，网络可能不能学习到B的内容。EWC则是对任务A中特别重要的限制较大，对不那么重要的参数限制较小。

约束选择

• 对于贝叶斯公式

  $$p(A|B) = \frac{p(A)p(B|A)}{p(B)}$$

  其中$p(A|B)$称为后验概率，$p(A)$为先验概率，一般来说，先验概率是对事件的初始判断，例如抛硬币的概率可以认为是0.5，而后验概率即由于制材等问题，实际观测中概率可能不是0.5。其中这些影响先验的信息即$B$，我们可以通过贝叶斯公式不断修正概率得到真实概率。

• EWC的目的是找到对于一个数据集$D$最重要的那些参数。假设这个参数为$\theta$，我们的优化目的即找到最大的后验概率（即在$D$中找到最优解$\theta$）

  $$\log p(\theta | D)$$

  然而我们不可能尝试每一个$\theta$, 所以我们可以通过贝叶斯公式转为先验概率

  $$\begin{aligned} \log p(\theta | D) &= \log \frac{p(\theta D)}{p(D)}\\ &= \log \frac{p(D|\theta)p(\theta)}{p(D)} \\ &= \log p(D|\theta) + \log p(\theta) - \log p(D) \end{aligned}$$

  假设$D$由两个相互独立的数据集$D_A,D_B$构成，上述公式可以转为

  $$\log p(\theta | D) = \log p(D_B | \theta) + \log p(\theta | D_A) - \log p(D_B)$$

  此时任务$D_B$的对数似然$\log p(D_B | \theta)$可以看成就是任务$B$的损失函数相反数（即取解$x = \theta$时预测值和真实值的残差，$\log$近似为取负），记其为$L_B(\theta)$。$\log p(D_b)$为常数，最终网络优化目标为

  $$\max(-L_B(\theta) + \log p(\theta | D_A))$$

拉普拉斯近似

• 上述目标函数取反得到最小化目标函数

  $$\min(L_B(\theta) - \log p(\theta | D_A))$$

  此时，我们得到了损失函数中的约束项即$D_A$的后验约束。但很显然我们依然无法求解该后验概率，EWC采用拉普拉斯近似的方式对该式进行替代。

• 令先验$p(D_A \mid \theta))$符合高斯分布$N(\mu, \sigma)$（即认为数据集$D_A$符合高斯分布），有

  $$p(D_A \mid \theta) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(\theta - \mu)^2}{2\sigma^2}}$$

  两边对数得

  $$\log p(D_A \mid \theta) = \log \frac{1}{\sqrt{2\pi}\sigma} - \frac{(\theta - \mu)^2}{2\sigma^2}$$

  令$f(\theta) = \log p(D_A \mid \theta)$，在$\theta = \theta^{*}_A$处进行泰勒展开，有

  $$f(\theta) = f(\theta^{*}_A) + f'(\theta_A^{*})(\theta - \theta_A^{*}) + f''(\theta_A^{*})\frac{(\theta-\theta_A^{*})}{2} + o(\theta^{*}_A)$$

  由于$\theta^{*}_A$为最优解，为驻点，则有

  $$\log \frac{1}{\sqrt{2\pi}\sigma} - \frac{(\theta - \mu)^2}{2\sigma^2} \approx f(\theta^{*}_A) + f''(\theta_A^{*})\frac{(\theta-\theta_A^{*})}{2}$$

  可解得$\mu = \theta_A^{*}, \sigma^2 = -\frac{1}{f''(\theta_A^{*})}$，又由贝叶斯公式可得后验概率同样符合高斯分布，则有

  $$p(\theta | D_A) \sim N(\theta_A^{*}, -\frac{1}{f''(\theta_A^{*})})$$

  由于$f(\theta_A^{*})$为常数，故我们的优化目标可以化为

  $$\min (L_B(\theta - f''(\theta_A^{*})\frac{(\theta - \theta_A^{*})^2}{2}))$$

费雪矩阵

• 最终二阶导的Hesse矩阵是一个$n\times n$阵，EWC使用费雪信息对角阵进行替代。

  费雪矩阵本身等于Hesse矩阵的负期望

  $$F_{ij} = -\mathbb{E}[f''(\theta_A^{*})]$$

  如果只取对角线元素有

  $$F_{ii} = -\mathbb{E}_{p(\theta |A)}\left[\frac{\partial^2 \log p(\theta|A)}{\partial \theta_i}\vert_{\theta =\theta_A^{*}}\right]^2$$

  最终，网络的损失函数为

  $$\mathcal{L} = L_B(\theta) + \frac{\lambda}{2}\sum_i F_i(\theta - \theta_{A,i}^{*})^2$$