Identity Mappings in Deep Residual Networks

• DOI: 10.1007/978-3-319-46493-0_38

• 深度残差网络表现出很好的分类准确率，该文是作者在原始ResNet的基础上分析了残差块背后的数学原理。

残差块

• 一个残差块可以表示为

  $$\mathbf{y}_l = h(\mathrm{x}_l) + \mathcal{F}(\mathbf{x}_l, \mathcal{W}_l),\\ \mathbf{x}_{l+1} = f(\mathbf{y}_l),\tag{1}$$

  其中$\mathbf{x}_l$代表第$l$个单元的输入，$\mathcal{F}$代表一个残差函数，$h(\mathbf{x_l}) = \mathbf{x}_l$是一个恒等映射，$f$代表ReLU。

• 该文不只是在残差单元内部分析，而是在整个网络中创建一个“直接”路径分析信息传播。结果表明如果$h$和$f$都是恒等映射，则在前向和反向阶段，信号可以直接从一个单元传递到其他任意一个单元。

分析

• 如果$f$也是一个恒等映射，则有

  $$\mathbf{x}_{l+1} = \mathbf{x}_l + \mathcal{F}(\mathbf{x}_l, \mathcal{W}_l)\tag{2}$$

  通过递归，对于任意深层单元$L$和任意浅层单元$l$有

  $$\mathbf{x}_L = \mathbf{x}_l + \sum_{i=l}^{L-1}\mathcal{F}(\mathbf{x}_i, \mathcal{W}_i),\tag{3}$$

  这有两个特性：

  1. 任意深层单元的特征$\mathbf{x}_L$都可以由浅层单元$\mathbf{x}_l$的特征加上形如$\sum\mathcal{F}$的残差函数。这说明任意单元$L$和$l$之间具有残差特性。
  2. 对于一个$L$层的深度网络，最后一层的特征$\mathbf{x}_L$是$\mathbf{x}_0$加上中间残差函数的结果。但对于非残差形式的普通网络则是矩阵相乘的形式，即$\mathbf{x}_L = \prod W_i\mathbf{x}_0$。

• 根据式3，设网络的损失函数表示为$\varepsilon$，我们求解其反向传播求导链为

  $$\frac{\partial \varepsilon}{\partial \mathbf{x}_l} = \frac{\partial \varepsilon}{\partial \mathbf{x}_L}\frac{\partial \mathbf{x}_L}{\partial \mathbf{x}_l} = \frac{\partial\varepsilon}{\partial \mathbf{x}_L}(1 + \frac{\partial}{\partial\mathbf{x}_l}\sum_{i=l}^{L-1}\mathcal{F}(\mathbf{x}_i, \mathcal{W}_i)).\tag{4}$$

  式4表明损失函数对输入的梯度可以分解为两项相加的结果，第一项损失函数对$\mathbf{x}_L$的偏导和权重层无关，第二项和权重层有关。$\frac{\partial\varepsilon}{\partial\mathbf{x}_L}$表明了信息可以直接回传到网络的任意浅层$l$。同时对于一个小批次训练集来说，由于不太可能训练集中的每一个训练样本的第二项都为-1，即整个梯度值不太可能为0，这样即使权重值很小的时候也不太可能发生梯度消失问题。

讨论

• 上述分析的基础是$h$和$f$都是恒等映射，作者在后续还分析了其他集中情形。

恒等跳跃连接的重要性

• 考虑使用将恒等连接$h$替换为$h(\mathbf{x}_l) = \lambda_l\mathbf{x}_l$，其中$\lambda_l$是一个可调节标量，同时$f$不变。此时对于任意深层单元$L$和浅层单元$l$有：

  $$\mathbf{x}_L = (\prod_{i=l}^{L-1}\lambda_i)\mathbf{x}_l + \sum_{i=l}^{L-1}\hat{\mathcal{F}}(\mathbf{x}_i, \mathcal{W}_i),\tag{5}$$

  其中$\hat{\mathcal{F}}$为$\mathcal{F}$和标量系数相乘的结果($\hat{\mathcal{F}}_i = (\prod_{j=i+1}^{L-1}\lambda_j)\mathcal{F}_i$)。此时损失函数对输入数据的偏导为

  $$\frac{\partial\varepsilon}{\partial \mathbf{x}_l} = \frac{\partial \varepsilon}{\partial \mathbf{x}_L}\left((\prod_{i=l}^{L-1}\lambda_i)+\frac{\partial}{\partial \mathbf{x}_l}\sum_{i=l}^{L-1}\hat{\mathcal{F}}(\mathbf{x}_i, \mathcal{W}_i)\right).\tag{6}$$

  对于式6，如果网络特别深且$\lambda_i>1$对于$\forall i \in [0, L-1]$成立。则第一项便会非常大将造成梯度爆炸，反过来如果$\lambda_i<1$，则这项便会非常小造成梯度消失。

• 除此之外作者还验证了其他几种跳跃连接方式，如图1所示。

  

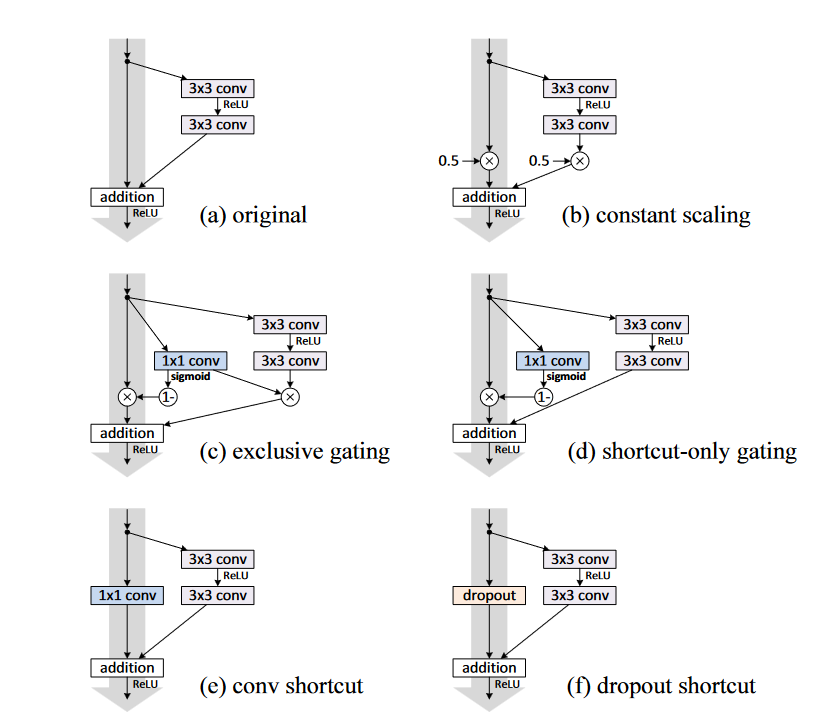
  图1. 多种跳跃连接方式。

  得到的结果如图2所示

  

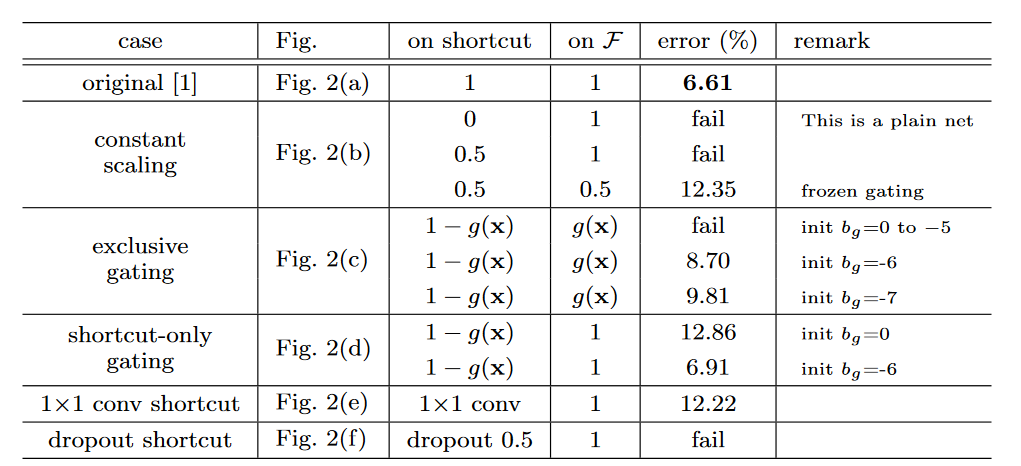
  图2. 测试结果（这里的Fig. 2在本文中指代图1）

  可以看到所有设置方式都不如直接恒等映射（可以看到添加一个$1\times 1$的卷积也会影响错误率）。理论上引入卷积等操作具有更强的表示能力，但实际误差高于恒等映射，这表明模型的退化问题是由优化问题造成的，而不是由表征能力造成的。

激活函数的使用

• 这一节讨论的是激活函数$f$如何使用，作者使用了如图3所示的集中架构来测试激活函数对残差网络的影响。

  

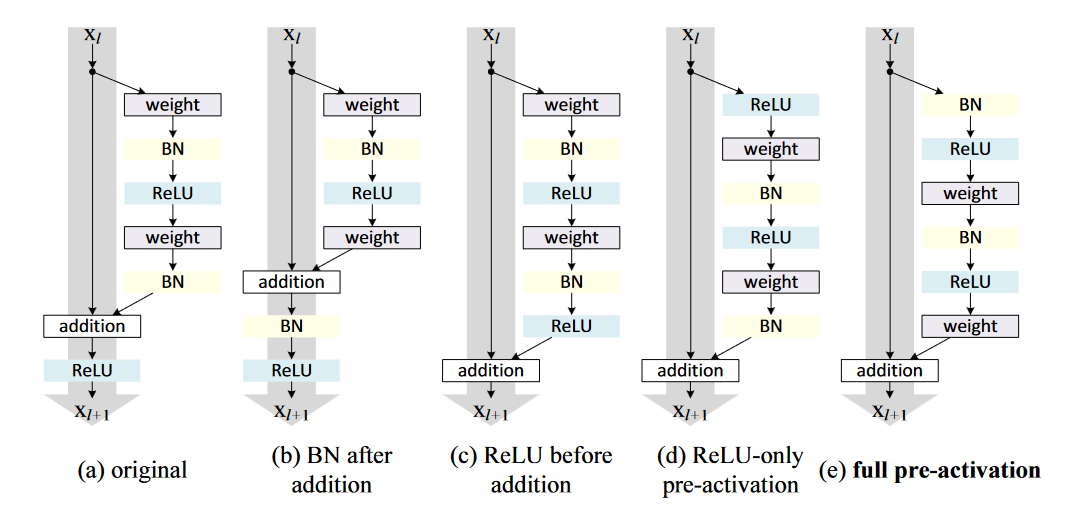
  图3. 不同激活函数的使用方式。

  得到的结果如图5所示

  

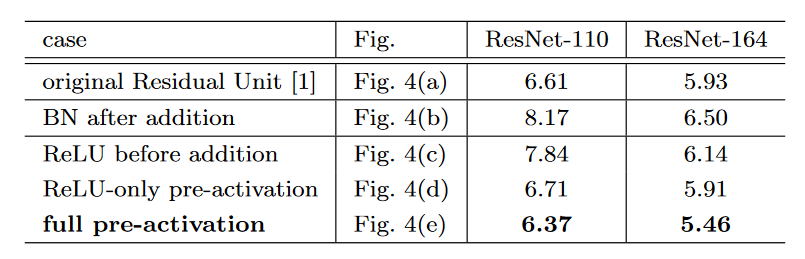
  图4. 测试结果（这里的Fig. 4在本文中指代图3）

• 首先可以发现在加操作之后引入BN会降低准确性，原因是因为BN层阻碍了信号传输。其次在加操作前引入额外的ReLU也影响模型的表示能力，因为这样使得得到的残差值为非负值（我们需要它处于负无穷至正无穷）。

  同时对于原始残差块中，激活函数在两条线路上影响着下一个残差单元，因为：

  $$\mathbf{y}_{l+1} = f(\mathbf{y}_l) + \mathcal{F}(f(\mathbf{y}_l), \mathcal{W}_{l+1}).\tag{7}$$

  即激活函数即影响快捷连接部分还影响残差函数部分，该文中重新设计了不对称的残差块，如图5 (b)所示，这样的好处是使得激活函数$\hat{f}$只影响残差部分，即

  $$\mathbf{x}_{l+1} = \mathbf{x}_l + \mathcal{F}(\hat{f}(\mathbf{y}_l), \mathcal{W}_{l+1}).\tag{8}$$

  

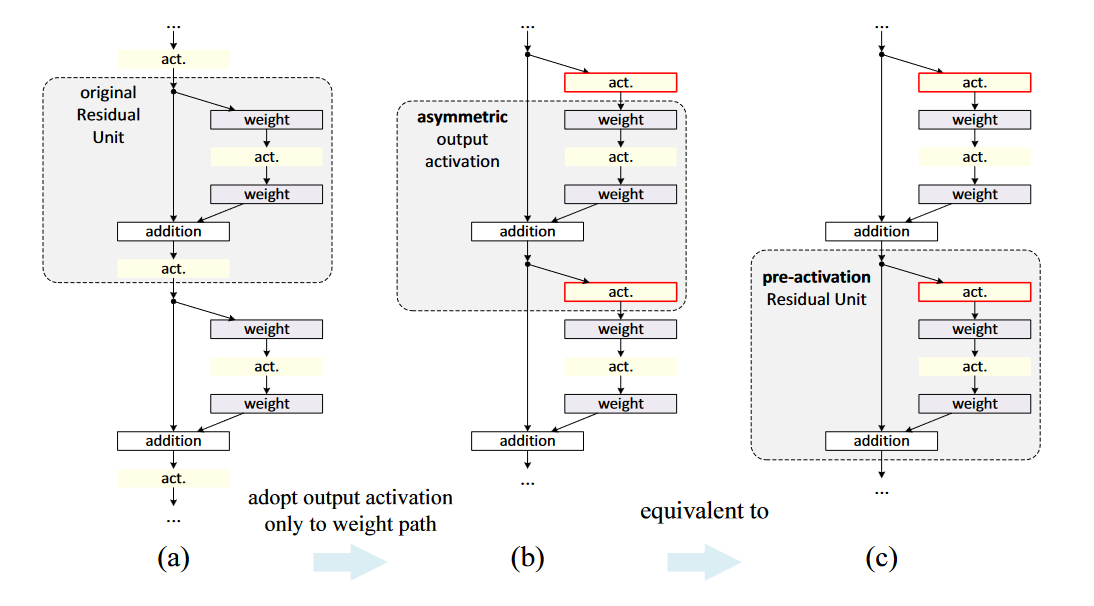
  图5. 新的残差块。

  还可以发现式 8与式 3类似，所以可以得到与式 4类似的反向方程。新的附加激活函数变成了一个恒等映射，优化变得更加容易。 这个设计还表明若激活函数$\hat{f}$是非对称的，等同于将$\hat{f}$作为下一个残差单元的预激活（pre-activation）项，如图5 (c)所示。这样的好处便是引入非对称的激活函数时还不破坏残差结构的优点。

• 同时由图4 可以看出全预激活比只将ReLU进行预激活更好。

总结

1. 数学上证明了残差结构消除了梯度消失和梯度爆炸的问题。
2. 设计新的残差结构使得引入ReLU、BN等优化结构时不破坏残差结构。