KAN: Kolmogorov–Arnold Networks

• arxiv链接：arxiv.org/abs/2404.19756

• 本文提出了基于KA（Kolmogorov Arnold）定理的K-A网络并与MLP进行比较。与MLP最大的不同是MLP在节点（神经元）上具有固定的激活函数，而KAN在边（权重）上具有可学习的激活函数。即KAN天生就不是线性权重——每个权重参数都被参数化为样条曲线的单变量函数所替代。

  本文发现这个改动使得KAN在准确性和可解释性方面要优于MLP。具体而言在数据拟合和PDE求解，更小的KAN便可以与一个大MLP取得相同的准确性。同时KAN可以直观的可视化，便于人工交互，即更好的可解释性。总而言之本文认为KAN非常有理由成为MLP的替代品。

知识补充

贝塞尔曲线

• 参考深入理解贝塞尔曲线

样条函数（spline）函数

• 分段光滑，各段交接处也一定光滑性的多段函数。用于插值或者拟合。

  和多项式函数的不同便是拟合（或者插值）时是分段操作的，即分为$n$个段，每个段单独拟合一条曲线，曲线与曲线（段与段）交接点在额外处理保证一定光滑性。

• 后续本文中的B-样条函数即贝塞尔曲线的一般形式，参考速通：贝塞尔曲线和B样条

  简单来说贝塞尔曲线就是基于分段的全局拟合，而B-样条中增加了支撑集的概念使得不会因为局部改动影响全部。

Introduction

图1.1 MLP vs. KAN

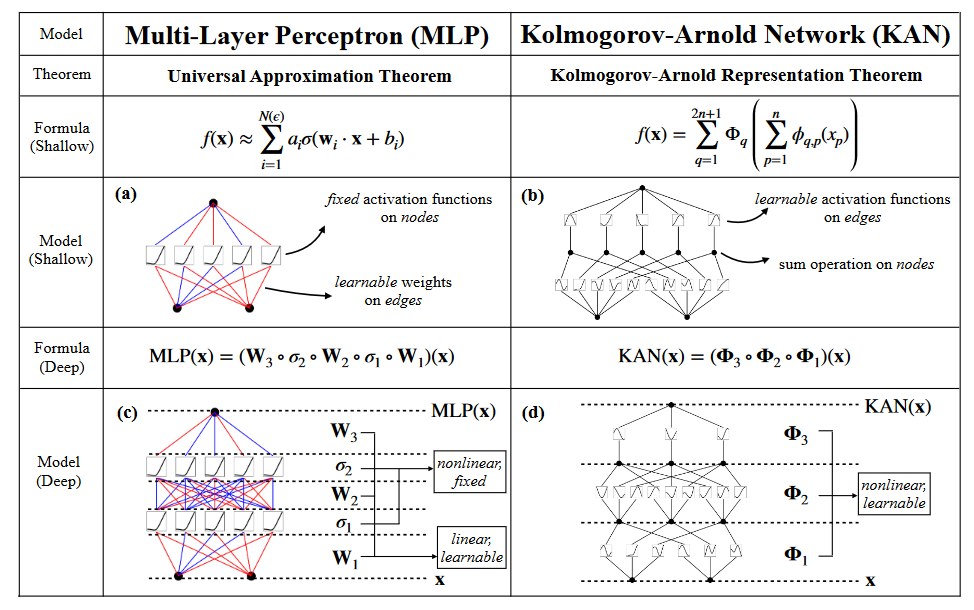
• 如图1.1可见MLP与KAN的不同，对于KAN而言不存在线性权重矩阵，每个权重参数都被参数化为可学习一维（单变量）样条函数替代。在KAN中节点只需要进行加权求和即可，而不需要在节点处使用激活函数。

  这里人们可能会担心权重参数变成样条函数后成本变高，但是本文提出因为KAN相比MLP只需要更小的模型，例如对于PDE求解，2层宽度10的KAN比4层宽度100的MLP精确100倍，参数效率高100倍。（所以实际成本可能不会增加反而有更多的好处）

  在更早之前也有很多关于基于KA的神经网络研究工作，不过都停留在2层宽度$2n+1$表示，而且没有用到现代技术（例如BP）训练网络。本文工作将KA表示推广到任意深度和宽度。

• 本文也承认KAN本质上是样条函数和MLP的组合，利用各自的优势避开各自的劣势。对于样条曲线而言其适用于低维函数，易于局部调整，但存在维数诅咒（COD）问题。对于MLP而言基于特征学习适用与高维，但在低维中不如样条函数精确。所以KAN对外（整体）上为MLP，内部具有样条函数，这种结构使得KAN不仅可以学习特征还可以准确优化这些学习的特征。例如对于高维函数

  $$f(x_1, \dots, x_N) = \exp\left(\frac{1}{N}\sum_{i=1}^N{\sin^2(x_i)}\right)\tag{1.1}$$

  由于COD的存在样条函数在$N$较大时将失效，而MLP则可以学习广义加性结构（generalized additive structure），不过对于使用ReLU来近似指数函数和正弦函数效率非常低（也就是为啥MLP要那么多参数）。所以KAN在这类情况中远远优于MLP。

图2.1 文章结构

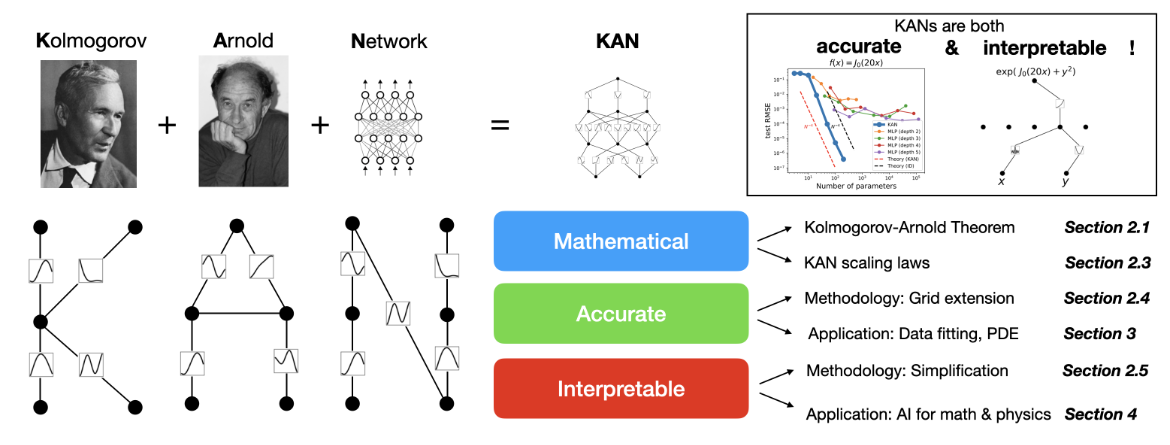
• 本文的结构如图2.1所示。第二节中将介绍KAN结构及数学基础。第三节展示数据拟合和PDE求解方面和MLP的对比。第四节展示KAN良好的可解释性。第五节中总结相关工作。第六节讨论KAN的影响和未来展望。

2 Kolmogorov–Arnold Networks (KAN)

2.1 Kolmogorov-Arnold Representation theorem

• Vladimir Arnold和Andrey Kolmogorov提出如果$f$是有界域上的多元连续函数，则$f$可以写成单变量连续函数和加法运算的有限组合。例如对于光滑函数$f:[0,1]^n\rightarrow\mathbb{R}$

  $$f(\mathbf{x}) = f(x_1, \cdots, x_n) = \sum_{q=1}^{2n+1}\Phi_q\left(\sum_{p=1}^n{\phi_{q,p}(x_p)}\right)\tag{2.1}$$

  其中$\phi_{q,p}:[0, 1]\rightarrow\mathbb{R}$且$\Phi_q:\mathbb{R}\rightarrow\mathbb{R}$。这代表只有加法是一个多变量函数（$f(x,y) = x+y$），因为其他所有函数都可以用单变量函数和加法进行表示。对于ML而言，这代表学习高维函数可能可以归约为学习多项式数量的一维函数。不过实际上是不行的，因为这些一维函数可能是非光滑的，甚至是分形的，也即在实践中可能是不可学习的。所以之前的工作都认为K-A表示在ML中基本没啥用（理论有用，实际无用）的状态。

• 本文乐观的认为K-A还是有用的，基于此做了两部分工作，一是将网络推广到任意宽度和深度，二是研究一般性任务中KAN的具体表现。

2.2 KAN architecture

图2.2 左：网络架构。右：参数化B样条函数以及两种粒度

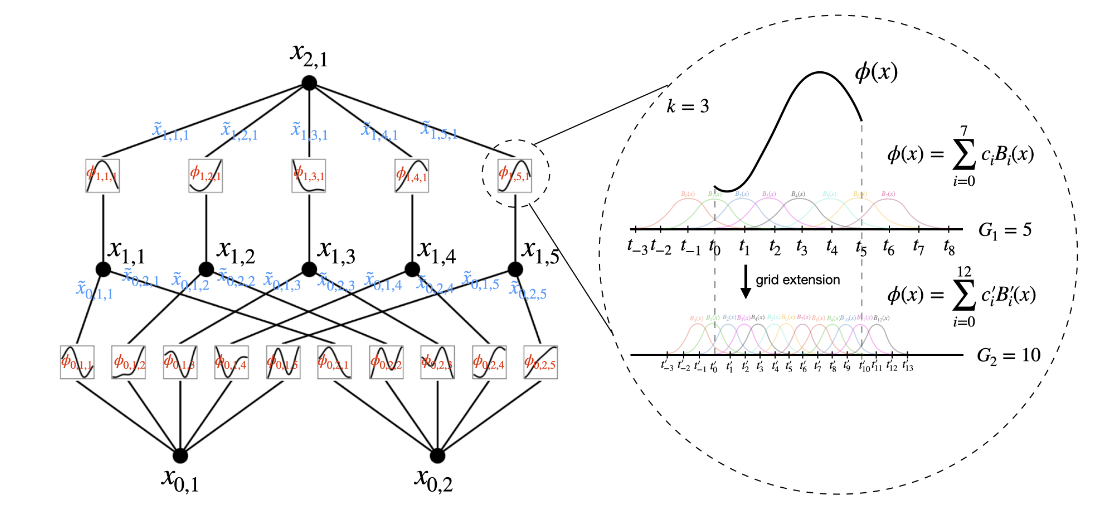
• 对于一组监督学习任务$\{\mathbf{x}_i, y_i\}$，我们想要找到函数$f$使得$y_i\approx f(\mathbf{x}_i)$对所有数据对成立。由式2.1可知如果能找到合适的单变量函数$\phi_{q,p},\Phi_q$便可以得到$f$。由此可以设计一个参数化方程的神经网络，即将每个要学习的单变量函数参数化为具有局部B-样条基的可学习系数B-样条函数（图2.2右侧）。这便是KAN的原型，计算图由式2.1指定，最终如图1.1(b)所示（n=2）的一个两层神经网络。

  本文的突破性工作便是结合MLP的多层结构，定义了KAN层——具有$n_{in}$维输入及$n_{out}$输出的KAN层由一维函数矩阵表示为

  $$\Phi = \{\phi_{q,p}\},\ p = 1,2,\dots,n_{in},\ q = 1,2,\dots,n_{out}\tag{2.2}$$

  其中$\phi_{q,p}$具有可训练参数，后续即可和MLP相同的方式（堆叠多个KAN层）来获得更深层的神经网络。

• 如图2.2(左)示，KAN形状可以由一个整数数组表示，

  $$[n_0,n_1,\cdots,n_L]\tag{2.3}$$

  其中$n_i$表示计算图第$i$层的节点数。用$(l,i)$-神经元代表第$l$层的第$i$个神经元，用$x_{l,i}$代表该神经元的激活值。在第$l$层与$l+1$层之间存在$n_ln_{l+1}$个激活函数，连接$(l,j)$和$(l+1,i)$的激活函数表示为

  $$\phi_{l,i,j},\ l = 0,\cdots,L-1, i = 1,\dots,n_{l+1},\ j=1,\dots,n_l\tag{2.4}$$

  同时$\phi_{l,i,j}$预激活（激活前的）值表示为$x_{l,i}$，后激活（激活后的）值表示为$\hat{x}_{l,i,j} \equiv \phi_{l,i,j}(x_{l,i})$。$(l+1,j)$-神经元的激活值为所有传入值的和

  $$x_{l+1,j} = \sum_{i+1}^{n_l}\hat{x}_{l,i,j} = \sum_{i+1}^{n_l}{\phi_{l,i,j}(x_{l,i})},\ j=1,\dots,n_{l+1}\tag{2.5}$$

  换成矩阵形式即

  $$\mathbf{x}_{l+1} = \underbrace{\begin{pmatrix} \phi_{l,1,1}(\cdot)&\phi_{l,1,2}(\cdot)&\cdots&\phi_{l,1,n_1}(\cdot)\\ \phi_{l,2,1}(\cdot)&\phi_{l,2,2}(\cdot)&\cdots&\phi_{l,2,n_1}(\cdot)\\ \vdots&\vdots&&\vdots\\ \phi_{l,n_{l+1},1}(\cdot)&\phi_{l,n_{l+1},2}(\cdot)&\cdots&\phi_{l,n_{l+1},n_1}(\cdot)\\ \end{pmatrix}}_{\Phi_l}\mathbf{x}_l\tag{2.6}$$

  用$\Phi_{i}$表示第$l$个KAN层的函数矩阵。常规KAN由$L$层组成：给定输入向量$\mathbf{x}_0\in\mathbb{R}^{n_0}$，KAN的输出为

  $$\mathrm{KAN}(\mathbf{x}) = (\Phi_{L-1}\circ\Phi_{L-2}\Phi_{L-1}\circ\cdots\circ\Phi_{1}\circ\Phi_{0})\mathbf{x}\tag{2.7}$$

Implementation details

• 虽然KAN层方程很简单，但是还需要一些优化技巧：

1. 残差激活函数（Residual activation functions）：选择一个基函数$b(x)$（类似残差连接），满足激活函数$\phi(x)$是基函数$b(x)$和样条函数之和

   $$\phi(x) = \omega(b(x)+\mathrm{spline}(x))\tag{2.8}$$

   其中

   $$b(x) = \mathrm{silu}(x) = x/(1+e^{-x})\tag{2.9}$$

   在大多数情况下样条函数$\mathrm{spline}(x)$被参数化为B-样条曲线的线性组合，满足

   $$\mathrm{spline}(x) = \sum_i{c_iB_i(x)}\tag{2.10}$$

   其中$c_i$是训练参数，$\omega$为权重因子。

2. 初始化

   每个激活函数初始化为$\mathrm{spline}(x)\approx 0$，$\omega$由Xavier初始化确定。

3. 样条网格更新

   样条曲线定义在有界区域上但激活值在训练过程中可能会从固定区域演化出来，所以这里选择根据输入激活值动态更新每个网格。

Parameter count

• 对于一个深度为$L$，每层宽度为$n_0=n_1=\cdots=n_L = N$，每个3次样条包含$G$段（$G+1$个格点）。

  则一共有$O(N^2L(G+k))\sim O(N^2LG)$个参数。同尺寸的MLP包含$O(N^2L)$个参数，但KAN大部分情况需要的尺寸比MLP更小且泛化能力更好。

2.3 KAN’s Approximation Abilities and Scaling Laws

• 在式2.1中，2层深度$2n+1$宽度的表示可能是非光滑的，而更深层表示可能会带来更平滑的激活值。例如一个4变量函数

  $$f(x_1,x_2,x_3,x_4) = \exp(\sin(x_1^2+x_2^2) + \sin(x_3^2 + x_4^2))\tag{2.11}$$

  可以由3层KAN$[4,2,1,1]$平滑表示，但是可能无法用具有平滑激活函数的2层网络来表示。为了便于近似分析，本文仍假设激活函数是平滑的，且允许表示层为任意宽度和深度。

• 定理2.1（近似定理KAT）：设$\mathbf{x} = (x_1,x_2,\cdots,x_n)$，函数$f(x)$代表一个表示层（类似式2.7）

  $$f = (\Phi_{L-1}\circ\Phi_{L-2}\circ\cdots\circ\Phi_1\circ\Phi_0)\mathbf{x}\tag{2.12}$$

  其中$\Phi_{l,i,j}$为$(k+1)$阶可微。则存在依赖于$f$的一个常数$C$，网格大小为$G$，有如下近似界：存在$k$阶B-样条函数$\Phi_{l,i,j}^G$满足对于任意$0\le m \le k$，有

  $$\lVert f - (\Phi_{L-1}^G\circ\Phi_{L-2}^G\circ\cdots\circ\Phi_1^G\circ\Phi_0^G)\mathbf{x} \rVert_{C^m} \le CG^{-k-1+m}\tag{2.13}$$

  这里使用$C^m$范数衡量$m$阶导数的大小，有

  $$\lVert g\rVert_{C^m} = \max\limits_{|\beta|\le m}\sup\limits_{x\in[0,1]^n}\lvert D^\beta g(x)\rvert$$

• 也就是说可以用有限网格大小的KAN进行拟合，而且误差与维数无关，从而摆脱COD问题。对于$C$是否和维度相关本文留给未来工作。

神经缩放定律

• 神经缩放定律是指测试损失随着模型参数增加而减少的现象（就是越大越好）。例如$\mathcal{l}\propto N^{-\alpha}$，其中$\mathcal{l}$为测试RMSE，$N$为参数数目，$\alpha$为缩放指数。

  在KAN中假设目标存在平滑的K-A表示，将高维函数分解为几个一维函数，则$\alpha = k+1$（$k$为阶数），后续在节3.1证明了$\alpha=4$也是最大最好的缩放指数。

Comparison between KAT and UAT

• 略

2.4 For accuracy: Grid Extension

• 理论上样条可以精确拟合目标函数，因为网格可以任意精细度，KAN也正是由此特性所以比MLP更好。而且对于KAN而言，可以先训练一个小网络，再用更精细的网格扩展到更多参数的KAN而无需重新训练。

  网格扩展（如图2.2右所示）的目的便是将新的粒度样条曲线拟合到旧的粒度样条曲线中。例如我们想用$k$阶样条拟合有界区域$[a,b]$中的一维函数$f$，具有$G_1$段的网格点为$\{t_0 = a, t_1,t_2,\cdots, t_{G_1} = b\}$，将其扩充为$\{t_{-k},\cdots,t_{-1},t_0,\cdots,t_{G_1},t_{G_1+1},\cdots,t_{G_1+k}\}$，其中包含$G_1+k$个B-样条基函数，且第$i$条B-样条$B_i(x)$仅在$[t_{-k+i},t_{i+1}],\ i=0,\dots,G_1+k-1$上非0.

  然后对于旧网格上的$f$将右这些B-样条基函数线性表示，$f_{\mathrm{coarse}}(x) = \sum_{i=0}^{G_1+k-1}{c_iB_i(x)}$。给定一个具有$G_2$段的精细网格，新网格上的$f$相应地为$f_{\mathrm{fine}}(x) = \sum_{i=0}^{G_1+k-1}{c_i^{'}B_i^{'}(x)}$。其中参数$c_j^{'}$将通过最小化$f_{\mathrm{fine}}(x)$到$f_{\mathrm{coarse}}(x)$之间的距离（最小二乘法实现）进行初始化。

  

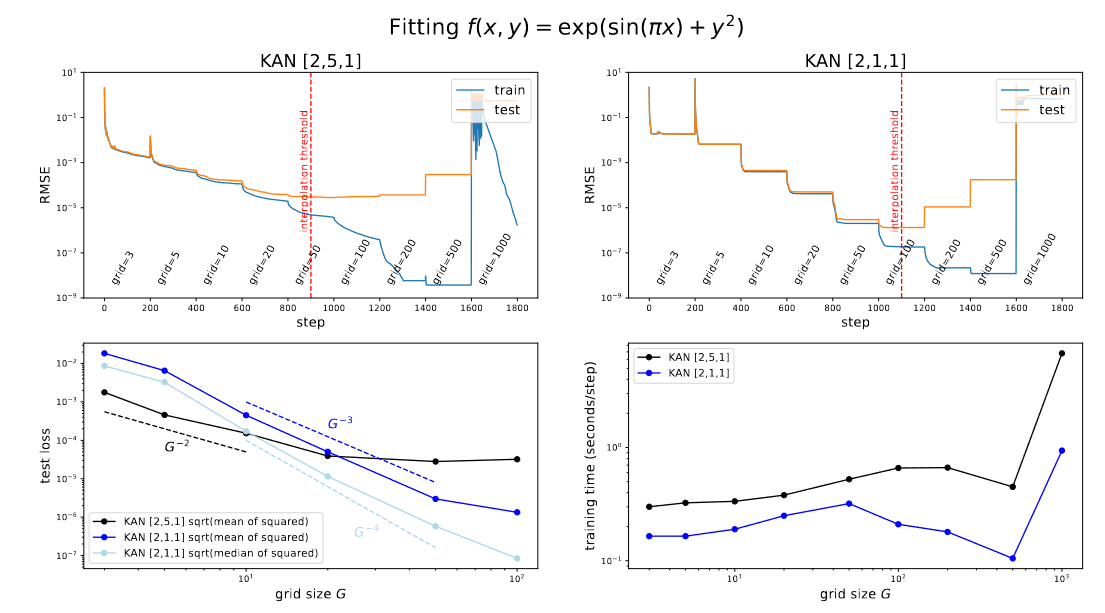
  图2.3 网格扩展

• 示例

  这里将使用不同的KAN来拟合$f(x,y) = \exp(\sin(\pi x) + y^2)$，结果如图2.3所示。可以看到随着网格增加训练和测试损失都减小，但当达到一定大小后，测试损失不降反增（过拟合）。而最后当网格达到1000时可能时由于优化算法由于损失函数地形不佳而停止工作。

  这里文中预计对于$[2,5,1]$KAN（包含$15G$个参数）将在$G=1000/15\approx 67$（1000为数据样本）处取插值阈值（图2.3中红色虚线）。

• Small KANs generalize better.

  在图2.3中可间，$[2,1,1]$KAN比$[2,5,1]$KAN有着更低的测试loss，而且其插值阈值更高（即泛化能力更强），这也是KAN中的关键问题，如何确定最小KAN形状？在本文节2.5中将给出一种通过正则化和修建来自动发现最小KAN架构的方法。

• Scaling laws

  这里探究测试loss和网格参数数量之间的关系，对于$[2,1,1]$KAN其尺度大致满足$\mathrm{test} \mathrm{RMSE}\propto G^{-3}$。根据定理2.1可知期望为$\mathrm{test} \mathrm{RMSE}\propto G^{-4}$。文中的解释时可能因为样本误差不均匀，所以图2.3中还放了误差中值得变化发现接近$G^{-4}$的尺度。

• External vs Internal degrees of freedom.

  KAN中的一个新概念是外部自由度和内部自由度之间的区别。节点连接方式的计算图表示外部自由度（"dofs"），激活函数内部的网格表示内部自由度。外部dofs负责学习多个变量组成的结构，内部dofs复杂学习单变量函数。

2.5 For Interpretability: Simplifying KANs and Making them interactive

• 这里的核心思想是训练一个足够大的KAN，再利用稀疏性正则化和修建进行训练。以及介绍了人工交互技术讨论KAN的可解释性。

简化技术

1. 稀疏化

   类似MLP引入正则项进行正则化的思想，不同的是KAN中需要两次修改。

   1. KAN没有线性“权重”（被可学习函数取代），所以需要重新定义L1范数。
   2. 本文发现L1不足以稀疏化KAN，所以这里选用增加熵进行正则化。

   本文定义对于$N_p$个输入的激活函数的L1范数为

   $$\lvert \phi\rvert_1 \equiv \frac{1}{N_p}\sum_{s=1}^{N_p}\left\lvert\phi(x^{(s)})\right\rvert\tag{2.14}$$

   对于具有$N_{\mathrm{in}}$个输入$N_{\mathrm{out}}$个输出的KAN层中的$\Phi$，将$\Phi$的L1范数定义为所有激活函数的L1范数和，即

   $$\lvert \Phi\rvert_1 \equiv \sum_{i=1}^{N_{\mathrm{in}}}\sum_{j=1}^{N_{\mathrm{out}}}\lvert\phi_{i,j}\rvert_1\tag{2.15}$$

   最后定义$\Phi$的熵为

   $$S(\Phi) \equiv -\sum_{i=1}^{N_{\mathrm{in}}}\sum_{j=1}^{N_{\mathrm{out}}}\frac{\lvert\phi_{i,j}\rvert_1}{\lvert\Phi\rvert_1}\log\left(\frac{\lvert\phi_{i,j}\rvert_1}{\lvert\Phi\rvert_1}\right)\tag{2.16}$$

   最终训练loss$\mathcal{l}_{total}$为预测损失$\mathcal{l}_{pred}$加L1和所有KAN层的熵正则项。

   $$\mathcal{l}_{total} = \mathcal{l}_{pred} + \lambda\left(\mu_1\sum_{l=0}^{L-1}\lvert \Phi_l\rvert_1 + \mu_2\sum_{l=0}^{L-1}{S(\Phi_l)}\right)\tag{2.17}$$

   其中$\mu_i$为正数通常$\mu_1 = \mu_2 = 1$，$\lambda$为超参数。

2. 可视化

   略

3. 修剪

   用稀疏化惩罚训练后，可以在节点上（而不是边上）进一步稀疏化KAN，对于每个节点定义传入传出的分数为

   $$I_{l,i} = \max\limits_{k}(\lvert\phi_{l-1,k,i})\rvert_1,\ \ O_{l,i} = \max\limits_{j}(\lvert\phi_{l+1,j,i}\rvert_1)\tag{2.18}$$

   如果传入传出分数大于都阈值则认为节点很重要，默认情况选择超参数$\theta = 10^{-2}$，小于阈值的节点将被修剪（删除）。

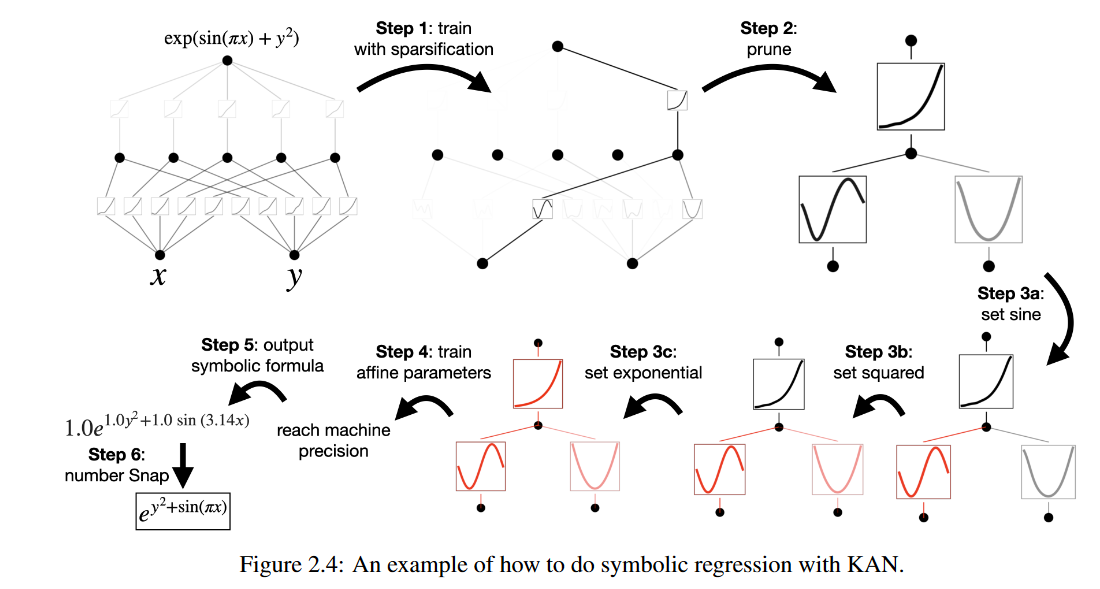
4. 符号化（Symbolification）

   当怀疑某些激活函数是符号时（指有名字，例如cos，log），KAN提供了一个接口将它们设置为指定的符号，例如fix_symbolic(l, i, j, f)代表将$(l, i, j)$激活函数设置为$f$。

图2.4 简化技术示例

个人总结

1. KAN与MLP的不同便是KAN中的激活函数从固定变成 -> 变动。

   具体变动的方法是使用$G$段的B-样条函数进行拟合。

   通过多层网络来将高维任务化简为多项式个一维任务。且由KAT解决了样条曲线COD问题（即误差足够小）。

2. 网格扩展技术

   使得训练时能够动态变换网格大小改变精度而无需重新设置参数从头训练。

3. 简化技术

   定义了新的正则项以及修剪技术简化网络。

4. 可解释性

   传统MLP是值的变化，所以遗忘和可解释性都是问题，个人认为本质还是数据维度的问题，单个值的信息太少了，纯靠堆参数。而KAN将学习参数变成一个函数，通过函数的变化更好的体现学习过程以及函数是可以再使用的。