一、PyTorch基础

• 环境安装请自己百度，这里不记录。

张量

• 张量（tensor）是torch中的数据结构，也是最基本的概念，一个张量本质就是一个多维数组，统一了标量、向量、矩阵的概念。

  

  张量

  在torch中一个张量包含以下8个属性。

  1. data：数据，带包装类的。

  2. dtype：张量数据类型。

  3. shape：张量的性质。一个n维列表，第i个代表第i维的元素个数。

  4. device：张量所在设备。

  5. grad：数据的梯度。

  6. grad_fn：张量生成的函数过程，如果是用户生成的则为None，依赖于其他张量生成时则为相应操作。通过它可以得到当前张量的梯度。

     就是记录张量的依赖关系，利用链式法则简化求梯度运算。

  7. requires_grad：是否需要梯度，不需要则不会记录自动生成的grad_fn属性。

  8. is_leaf：是否为叶节点。

• torch创建张量

  torch.tensor() # 直接创建
  torch.from_numpy() # 从np创建
  torch.zeros() # 根据大小创建全0的张量
  torch.ones() # 根据大小创建全1的张量
  torch.full() # 根据大小创建自定义填充的张量
  torch.arange(start, end) # range语法创建一维张量。
  torch.linspace() # 创建均分的1维张量，闭区间。
  torch.logspace() # 创建对数均分的1维张量，闭区间。
  torch.eye() # 创建单位对角矩阵。
  torch.normal(mean, std) # 高斯分布
  torch.bernoulli(mean, std) # 伯努利分布
  

• torch操作、运算，这些就不写了，不知道就找文档就行，基本你想要的操作/运算都是实现好的了，别想着自己写个函数。

自动梯度

• 这是PyTorch训练的核心，PyTorch中的自动梯度系统将会沿着反向传播自动更新梯度。

  实现原理也就是每次从张量运算得到新的张量时会记录运算操作，然后在某个值处调用backward，便会从这个张量开始更新上一级张量的梯度，并继续沿着上一级张量的生成链继续更新。

  不需要我们手动计算公司对具体张量计算梯度，同时利用链式法则减少了大量的运算量（类似记忆化搜索，中间变量多次复用），具体请看结尾的代码。

• 同时自动求导时只会保留叶子节点的梯度，即is_leaf=True节点的梯度，其他中间节点的梯度会被释放，如果想要保留中间节点的梯度，可以在反向传播前调用a.retain_grad()即可保留a张量的梯度。

概念

• 这里介绍一些训练中最基本的概念

  1. epoch：训练周期，一个周期代表模型使用了训练集的所有数据并且更新参数。
  2. batch_size：批次大小，一个样本子集，也就是从上次计算损失更新梯度到这次之间训练的数据量。
  3. batch：批次，也就是一组数据，数据量由batch_size决定。

• 放个线性回归的例子

  手动实现

  import torch
  from torch import nn
  import torch.optim as optim
  import torch.utils.data as Data
  import matplotlib.pyplot as plt
  
  class linear_regression(nn.Module):
      """
          线性回归类
          y = wx + b
      """
      def __init__(self):
          super().__init__()
          self.weight = torch.randn(1, requires_grad=True) # 权重初始值，这里设了个正态分布随机值
          self.bias = nn.Parameter(torch.randn(1))
          '''
              偏移初始值，这里换了个写法，Parameter包装也就是加上requires_grad一样的
              要requires_grad是因为需要对参数求梯度更新参数
          '''
      
      def forward(self, x):  # 预测
          _y = torch.add(torch.mul(x, self.weight), self.bias) # 记得别用python的操作符，当然你重载以下也行
          return _y
  
  class gradient_descent:
      """梯度下降"""
  
      def __init__(self, *params, lr) -> None:
          self.params = params
          self.lr = lr  # 学习率
      
      def zero_grad(self):
          """将梯度赋值为0"""
          for param in self.params:
              if param.grad is not None:
                  param.grad.zero_()
      
      def step(self):
          """更新梯度"""
          with torch.no_grad():
              '''
                  torch.no_grad() 代表下面的运算不要计算梯度，一是因为我们这里更新参数值，所以固定住梯度。二是减少不必要的运算。
              '''
              for param in self.params:
                  if param.grad is not None:
                      param -= self.lr * param.grad
  
  
  class MSELoss:
      """MSE损失函数"""
      def __call__(self, outputs, targets):
          diff = outputs - targets
          loss = diff ** 2
          mean_loss = loss.mean()
          return mean_loss
  
  
  # 随机生成点数据
  x = torch.rand(100,1)
  y = 2 * x + torch.rand(1)
  
  # 转换为TensorDataset并加载到DataLoader
  dataset = Data.TensorDataset(x, y)
  dataloader = Data.DataLoader(dataset, batch_size=10, shuffle=True)
  
  model = linear_regression()
  criterion = MSELoss()
  optimizer = gradient_descent(model.weight, model.bias, lr=0.01)
  
  for epoch in range(200):
      for inputs, labels in dataloader:
          optimizer.zero_grad()  # 清除梯度数据，这样才能重新训练
          outputs = model(inputs)
          loss = criterion(outputs, labels)  # 计算损失
          loss.backward()  # 反向传播
          optimizer.step()  # 使用优化器更新权重
      if (epoch+1) % 50 == 0:
          plt.plot(x.data.numpy(), model.weight.item() * x.data.numpy() + model.bias.item(), label=f'epoch_{epoch}')
  
  # 输出最终的拟合线参数
  print("Weight:", model.weight.item())
  print("Bias:", model.bias.item())
  
  # 可视化数据和拟合线
  plt.scatter(x.data.numpy(), y.data.numpy())
  plt.legend()
  plt.xlabel('x')
  plt.ylabel('y')
  plt.show()
  

  调包

  这里便是直接使用torch中已经定义好的各类模块（线性网络、MSE损失函数、随机梯度下降）直接进行训练。

  import torch
  from torch import nn
  import torch.optim as optim
  import torch.utils.data as Data
  import matplotlib.pyplot as plt
  
  
  # 随机生成点数据
  x = torch.rand(100,1)
  y = 2 * x + torch.rand(1)
  
  # 转换为TensorDataset并加载到DataLoader
  dataset = Data.TensorDataset(x, y)
  dataloader = Data.DataLoader(dataset, batch_size=10, shuffle=True)
  
  model = nn.Linear(1, 1)
  criterion = nn.MSELoss()
  optimizer = optim.SGD(model.parameters(), lr=0.01)
  
  for epoch in range(200):
      for inputs, labels in dataloader:
          optimizer.zero_grad()  # 清除梯度数据，这样才能重新训练
          outputs = model(inputs)
          loss = criterion(outputs, labels)  # 计算损失
          loss.backward()  # 反向传播
          optimizer.step()  # 使用优化器更新权重
      if (epoch+1) % 50 == 0:
          plt.plot(x.data.numpy(), model.weight.item() * x.data.numpy() + model.bias.item(), label=f'epoch_{epoch}')
  
  # 输出最终的拟合线参数
  print("Weight:", model.weight.item())
  print("Bias:", model.bias.item())
  
  # 可视化数据和拟合线
  plt.scatter(x.data.numpy(), y.data.numpy())
  plt.legend()
  plt.xlabel('x')
  plt.ylabel('y')
  plt.show()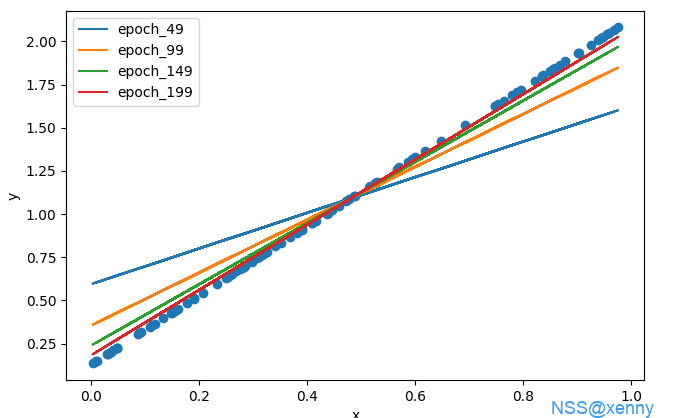
  

  

  结果

  可以看出随着训练周期增加，拟合得到的直线不断逼近真实情况。

• 可以看出一次训练的核心便是

  1. 清空梯度信息；
  2. 用输入进行预测；
  3. 用预测结果和真实结果计算损失；
  4. 通过损失反向传播更新梯度；
  5. 通过梯度下降更新权重参数。

  后续使用写其他算法也离不开这个过程，只是里面使用的具体模型、损失函数、优化器等等会有不同而已。