扩散模型（Diffusion model）

• GAN的本质是将生成器的分布逼近真实分布。VAE则是训练两个分布$q, p$分别表示从真实数据到噪声和噪声到生成数据的映射。

  扩散模型和VAE类似，也是一套从真实数据到噪声的分布以及噪声到生成数据的分布，但是在扩散模型中将这个过程分成了$T$步。

  

  四种生成方式

  扩散模型包含两个部分：扩散和和逆扩散过程。

扩散

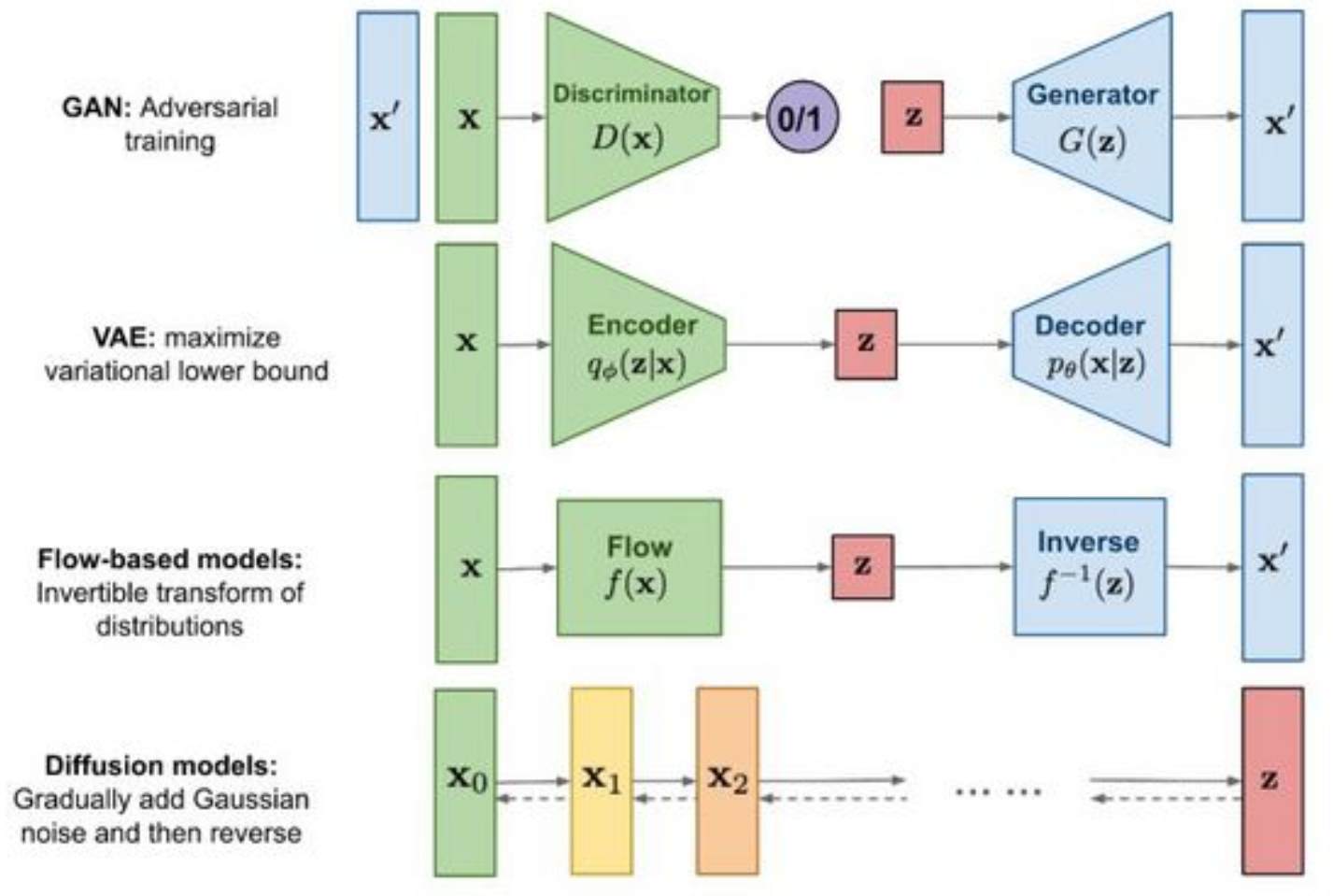
• 在这个过程中，原始图像$\mathbf{x}_0$会被添加$T$次噪声，使得$x_T$符合标准正态分布。

  但是这里的加噪声不是直接在上一张图片上“增加”（即修改数值）噪声值，而是定义一个均值和上一步图像有关的正态分布，再从该分布中采样得到下一张图像。即

  $$\mathbf{x}_t \sim \mathcal{N}(\mu_t(\mathbf{x}_{t-1}), \sigma_t^2\mathbf{I})\tag{1}$$

  大部分的扩散模型将这个正态分布设置为

  $$\mathbf{x}_t \sim \mathcal{N}(\sqrt{1-\beta_t}\mathbf{x}_{t-1}, \beta_t\mathbf{I})\tag{2}$$

  其中$\beta_t < 1$，且$\{\beta\}_{i=1}^T$一般为一个递增序列，目的是为了随着$t$的增加，$\mathbf{x}_t$越来越接近纯噪声$\mathcal{N}(0,\mathbf{I})$。 同时我们可以推导得到通项公式使得能够从$\mathbf{x}_0$直接计算$\mathbf{x}_t$。

  设$\epsilon_{t-1}$为标准正态分布，有$\mathbf{x}_t = \sqrt{1-\beta_t}\mathbf{x}_{t-1} + \sqrt{\beta_t}\epsilon_{t-1}$，则

  $$\begin{aligned} \mathbf{x}_t &= \sqrt{1-\beta_t}\mathbf{x}_{t-1} + \sqrt{\beta_t}\epsilon_{t-1} \\ &= \sqrt{1-\beta_t}(\sqrt{1-\beta_{t-1}}\mathbf{x}_{t-2} + \sqrt{\beta_{t-1}}\epsilon_{t-2}) + \sqrt{\beta_t}\epsilon_{t-1} \\ &= \sqrt{(1-\beta_t)(1-\beta_{t-1})}\mathbf{x}_{t-2} + \sqrt{(1-\beta_t)\beta_{t-1}}\epsilon_{t-2} + \sqrt{\beta_t}\epsilon_{t-1}\\ &= \sqrt{(1-\beta_t)(1-\beta_{t-1})}\mathbf{x}_{t-2} + \sqrt{1-(1-\beta_t)(1-\beta_{t-1})}\epsilon \end{aligned}\tag{3}$$

  令$\alpha_t = 1-\beta_t, \bar{\alpha_t} = \prod_{i=1}^t{\alpha_i}$，我们最终可以得到通项公式

  $$\mathbf{x}_t = \sqrt{\bar{\alpha_t}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha_t}}\epsilon\tag{4}$$

逆扩散

• 逆扩散便是使用神经网络学习每一步的噪声分布，我们希望能够得到每一次加噪声的逆操作，这样便可以实现从噪声中生成一张接近真实分布的图像。

  当$\beta_t$足够小（还没看是多足够）时，每一步的去噪声也满足正态分布，即我们可以从一个正态分布中的得到上一步的图像。

  $$\mathbf{x}_{t-1} \sim \mathcal{N}(\tilde{\mu}_t, \tilde{\beta}_t\mathbf{I})\tag{5}$$

  其中，$\tilde{\mu}_t,\tilde{\beta}_t$由步骤$t$，和$\mathbf{x}_t$决定。

计算

• 当我们已知$\mathbf{x}_0$时，每个步骤的方差$\tilde{\beta}_t$可由贝叶斯公式直接计算。

  令第$t$步的加噪分布为$q(\mathbf{x_t}|\mathbf{x}_{t-1})$，由贝叶斯公式有

  $$q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0) = q(\mathbf{x_t}|\mathbf{x}_{t-1},\mathbf{x}_0)\frac{q(\mathbf{x_{t-1}}|\mathbf{x}_0)}{q(\mathbf{x_t}|\mathbf{x}_0)}\tag{6}$$

  联立式 (4), (6)，可得

  $$\begin{aligned} \tilde{\beta}_t &= \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\cdot \beta_t\\ \tilde{\mu}_t &= \frac{1}{\sqrt{\alpha_t}}(\mathbf{x}_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_t) \end{aligned}\tag{7}$$

  此时我们可以发现，只有$\epsilon_t$为未知量，所以对于神经网络只需拟合噪声$\epsilon_{\theta}(\mathbf{x}_t,t)$。

损失函数

• 对于一轮训练，损失函数即为拟合的噪声与真实噪声的差值

  $$\mathcal{L} = \lVert \epsilon_t - \epsilon_\theta(\mathbf{x}_t, t)\rVert ^2 \tag{8}$$

总结

1. 本质上还是训练一个接近真实分布的分布。

2. 实际写代码训练时，每个epoch随机选取一个$T$，扩散到第$T$步得到$\mathbf{x}_T$再逆扩撒得到$\mathbf{x}_0$。

   扩散可以通过预计算$\alpha$的方式直接一步到位，逆扩散需要每步单独进行，所以扩散模型训练时间较慢。

3. 和其他生成模型一样，扩散模型本身是一种方法，并不关心具体神经网络，可以在具体任务中设计更适合的网络架构。